Obstacles in Chaining

Though it is desirable to select stations so as to avoid obstacles, occasionally the obstacles are unavoidable.

Various obstacles to chaining may be grouped into:
(i) Obstacles to ranging (chaining free-vision obstructed)
(ii) Obstacles to chaining (chaining obstructed-vision free)
(iii) Obstacles to both ranging and chaining.

Various methods of overcoming these obstacles are explained is this article.
Obstacles to Ranging

These obstacles can be further classified into the following categories:
(a) Both ends of the line are visible from some intermediate points. Intervening ground is an example of such obstacle. By resorting to reciprocal ranging this difficulty can be overcome.
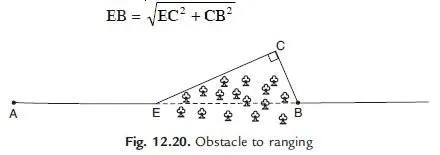
(b) Both ends of the line may not be visible from intermediate points on the line, but may be visible from a point slightly away from the line. Intervening trees and bushes are the examples of such obstacles. This obstacle to chaining may be overcome by measuring along a random line as shown in Fig. 12.20. In this case required length

Obstacles to Chaining
In this type the ends of lines are visible but chaining is obstructed. Examples of such obstructions are ponds, lakes, marshy land etc. Various geometric properties may be used to find obstructed length CB as shown in Fig. 12.21.

From eqn. (a), cos θ can be found and substituting it in eqn. (b), the obstructed length CB can be found.

Obstacles to Both Chaining and Ranging
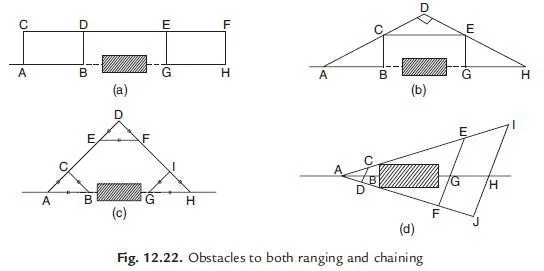
Building is a typical example of this obstacle. Referring to Fig. 12.22, line AB is to be continued beyond the obstacle, say as GH. Four possible methods are presented below:
(a) Set perpendiculars AC, BD such that AC = BD [Fig. 12.22 (a)]. Extend line CD to F. Drop perpendiculars EG and FH to line CF such that EG = FH = AC. GH is the continuation of line AB and DE = BG.
(b) Referring to Fig. 12.22 (b), set BC ⊥ to AB. Select D on extended line of AC. Set perpendicular DH such that AD = DH. Select point E on DH such that DE = DC. Then arcs of length EG = BC and arc of length HG = AB are drawn from E and H respectively and G is located. GH is continuation of AB and BG = CE. (c) Referring to Fig. 12.22 (c), C is located such that AC = BC = AB. Extend AC to D and construct equilateral triangle DEF. Extend DF to H such that DH = DA. Locate convenient point I on HD and construct equilateral triangle to locate G. Then GH is the continuation of line AB and length BG
is given by
BG = AH AB GH = AD AB GH

(d) In the method shown in Fig. 12.22 (d), points C and D are selected such that CBD is in a line.
Extend AC to E and I such that AE = n × AC and AI = m × AC. Similarly Extend AD to F and J such that, AF = n × AD and AJ = m × AD. Locate G and H on lines EF and IJ such that, EG = n × BC and IH = m × BC. Then GH is the continuation of line AB. Now, AG = n × AB ∴ BG = n × AB AB = (n 1) AB
Example 12.1: In chaining past a pond, stations C and B were taken on the opposite sides of the pond. A line DCE was set by selecting CD = 220 m and CE = 280 m. The lines DB and ED which are on the opposite sides of the pond are measured. If DB = 500 m and EB = 600 m, find obstructed length CD.
Solution: Referring to Fig. 12.21 ( f ),