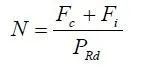In composite floors that need checking for vibration, damping is sufficiently low for its influence on natural frequencies to be neglected. For free elastic vibration of a beam or one-way slab of uniform section, the fundamental natural frequency is

Values for other end conditions and multi-span members are given by Wyatt. The relevant flexural rigidity is El (pre unit width, for slabs), L is the span, and m the vibrating mass per unit length (beams) or unit area (slabs). Concrete in slabs should normally be assumed to be uncracked, and the dynamic modulus of elasticity should be used for concrete, in both beams and slabs. This modulus, Ecd, is typically about 8 kN/mm2 higher than the static modulus, for normal-density concrete, and 3 to 6 kN/mm2 higher, for lightweight-aggregate concretes of density not less than 1800kg/m3. For composite beams in sagging bending, approximate allowance for these effects can be made by increasing the value of I for variable loading by 10%.
Unless a more accurate estimate can be made, the mass m is usually taken as the mass of the characteristic permanent load plus 10% of the characteristic variable load. A convenient method of calculating f0 is to find first the midspan deflection, m δ say, caused by the weight of the mass m. For simply-supported members this is
For a single-span layout of the type shown in Fig.3.1, each beam vibrates as if simply-supported, so the length Leff of the vibrating area can be taken as the span, L. The width S of the vibrating area will be several times the beam spacing, s. A cross-section through this area is likely to be as shown in Fig. 3.27, with most spans of the composite slab vibrating as if fixed-ended. It follows from equation (3.95) that:
for the beam,
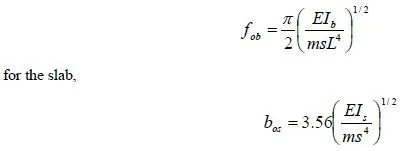
where m is the vibrating mass per unit area, and s is the spacing of the beams, and subscripts b and
s mean beam and slab, respectively.