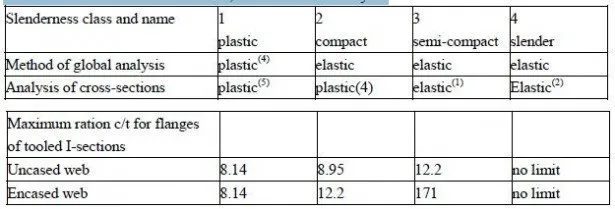
The effectiveness of shear connection is studied by means of loading tests on simply by means of loading tests on simply-supported composite slabs, as sketched in Fig 2.19 Specifications for such tests are given in Section 10.3 of Eurocode4 and in BS 5950:Part 4.(27) The length of each shear span, Ls is usually L/4,where L is the span ,which is typically about 3.0m. There are three possible modes of failure
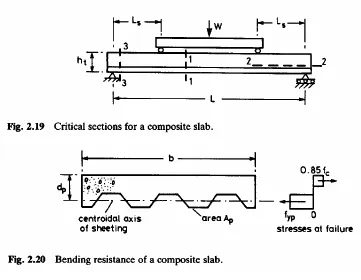

The expected mode of failure in a test depends on the ratio of a L to the effective depth p d of the slab, shown is Fig 2.20 In tests to Eurocode 4. the results are plotted on a diagram with axes V/bdp and Ap/bl. (Fig. 2.21) for reasons that are now explained
Mu = VLs
At high L/d flexural failure occurs The maximum bending moment. Mu is given by Where V is the maximum vertical shear, assumed to be much greater than the self-weight of the slab A sest specimen of breadth b should include a member of complete wavelengths of sheeting of total cross-sectional area Ap Flexural filure is modeled by simple plastic theory with all the steel at its yield stress fyp (Fig 2.20) and sufficient concrete at 0.85fc where fc is the cylinder strength for longitudinal equilibrium. The lever arm is a little less than dp but approximately.
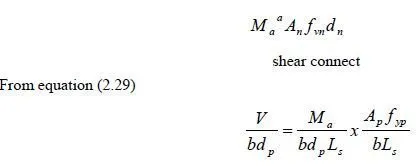
The strength yp f is not varied during a series of tests and has no influence on longitudinal shear failure It is therefore omitted from the aves on Fig.2.21 and equation (2.31) shows that flexural failure should plot as a straight line through the origin.
At low p L / d vertical shear failure occurs The mean vertical shear stress on the concrete is roughly equal to p Ap // b has little influence on its ultimate value so vertical shear failures are represented by a horizontal line on Fig 2.21 However, Patrirck and Bridge(18)have shown that this should be a rising curve.
Longitudinal shear failures occur at intermediate values of L/dp and lie near the line

as shown by AB on Fig 2.21 where M and K are constants to be deter-mined by testing Design based on equation (2.32)is one of the two methods given in Eurocode 4.(The other is treated in Section3.32).The present method is similar to one that has been widely used for several decades,(27-29)known as the m=k method In that method, m and k are usually defined by the equation
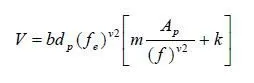
where fe is the measured cylinder or cube strength of the concrete. This equation can give unsatisfactory results for m and k when fe varies widely within a series of tests so fe has omitted from equation (2.32).A comparison of the two methods (15) has shown that this has little effect on m; but the two equations give different values for k in different units. A value found by ,for example the method of BS 5950; Part 4cannot be used in design to Euro code 4;but a new value can be determined from the original test data.
A typical set of tests consists of a group of three with L/dip such that the results lie near point Avon Fig 2.21 and a second group with lower L/d such that the results line near point B Values of m and k are found for a line drawn below the lowest result in cache group at a distance that allows for the scatter of the test data.
All six failures have to be in longitudinal shear; There failures typically commence when a crack occurs under of the load points, associated with loss of bond along the shear span and measurable Slip at the and of the span If this leads to failure of the slab the shear Connection is classified art brittle such failures occur suddenly and are penalized in design Eurobond 4 boa 20% reduction in design resistance.
Where the eventual failure load exceeds the load causing the first end slip by more than 10% the failure is classified as ductile Recently-earlier shapes which relied morc on frictional interlock and were more susceptible to brittle failure. The influence of bond is minimized in the standard test by the application of several thorsand eycles of repeated loading up to 1.5 times the expected loading in service before loading to failure.
When a new profile is developed, values of m and k have to be deter-mined in principle for each thickness of sheeting, each overall depth of slab to be used, and for a range of concrete strengths Cohes allow some simplification but the testing remains a long and costly process The m-k test is also unsatisfactory in other ways (15.30)A test using much smaller specimens, that may in time replace it ,is now described.