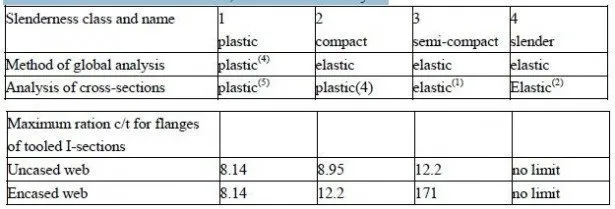
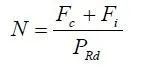In the preceding examplem the stress normal to the interface AOB (Fig.2.2) was everywhere compressive and equal to w/2b except at the ends of the beam .The stress would have been tensile if the load w had been applied to the lower member. Such loading is unlikely, except when traveling cranes are suspended from the steelwork of a composite floor above: but there are other situations in which stresses tending to cause uplift can occur at the interface. These arise from complex effects such as the torsional stiffness of reinforced concrete slabs forming flanges of composite beams, the triaxial stresses in the vicinity of shear connectors and, in box-girder bridges, the torsional stiffness of the steel box.
Tension across the interface can also occur in beams of non-uniform, Section or with partially completed flanges. Two members without shear connection, as shown in Fig. 2.5,provide a simple example. AB. Is sup-ported on CD and carries distributed loading. It can easily be shown by elastic theory that if the flexural rigidity of AB exceeds about one-tenth of that of CD, then the whole of the load on AB is transferred to CD at points A and B, with separation of the beams between these points. If AB was connected to CD, there would be uplift forces at midspan.
Almost all connectors used in practice are therefore so shaped that they provide resistance to uplift as well as to slip. Uplift forces are so much less than shear forces that it is not normally necessary to calculate or estimate them for design purposes, provided that connectors with some uplift resistance are used.