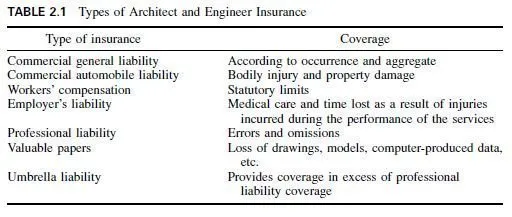
Design of bracing to resist forces induced by wind, seismic disturbances, and moving
loads, such as those caused by cranes, is not unlike, in principle, design of members that support vertical dead and live loads. These lateral forces are readily calculable. They are collected at points of application and then distributed through the structural system and delivered to the ground. Wind loads, for example, are at each floor level and distributed to the columns that are selected to participate in the system. Such loads are cumulative; that is, columns resisting wind shears must support at any floor level all the wind loads on the floors above the one in consideration.
Bracing Tall Buildings
If the steel frame of the multistory building in Fig. 7.16a is subjected to lateral wind load, it will distort as shown in Fig. 7.16b, if the connections of columns and beams are of the standard type, for which rigidity (resistance to rotation) is nil. One can visualize this readily by assuming each joint is connected with a single pin. Naturally, the simplest method to prevent this distortion is to insert diagonal members triangles being inherently rigid, even if all the members forming the triangles are pin-connected.
Braced Bents. Bracing of the type in Fig. 7.16c, called X bracing, is both efficient and economical. Unfortunately, X bracing is usually impracticable because of interference with doors, windows, and clearance between floor and ceiling. Usually, for office buildings large column-free areas are required. This offers flexibility of space use, with movable partitions. But about the only place for X bracing in this type of building is in the elevator shaft, fire tower, or wherever a windowless wall is required. As a result, additional bracing must be supplied by other methods. On the other hand, X bracing is used extensively for bracing industrial buildings of the shed or mill type.
Moment-Resisting Frames. Designers have a choice of several alternatives to X bracing. Knee braces, shown in Fig. 7.16d, or portal frames, shown in Fig. 7.16e, may be used in outer walls, where they are likely to interfere only with windows. For buildings with window walls, the bracing often used is the bracket type (Fig. 7.16Æ’). It simply develops the end connection for the calculated wind moment.
Connections vary in type, depending on size of members, magnitude of wind moment, and compactness needed to comply with floor-to-ceiling clearances.
Figure 7.17 illustrates a number of bracket-type wind-braced connections. The minimum type, represented in Fig. 7.17e, consists of angles top and bottom: They are ample for moderate-height buildings. Usually the outstanding leg (against the column) is of a size that permits only one gage line. A second line of fasteners would not be effective because of the eccentricity. When greater moment resistance is needed, the type shown in Fig. 7.17b should be considered. This is the type that has become rather conventional in field-bolted construction. Figure 7.17c illustrates the maximum size with beam stubs having flange widths that permit additional gage lines, as shown. It is thus possible on larger wide-flange columns to obtain 16 fasteners in the stub-to-column connection.
The resisting moment of a given connection varies with the distance between centroids of the top and bottom connection piece. To increase this distance, thus increasing the moment, an auxiliary beam may be introduced as shown in Fig. 7.17d, if it does not create an interference.
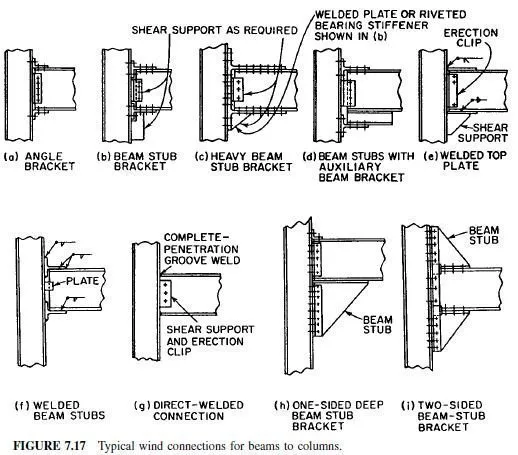
All the foregoing types may be of welded construction, rather than bolted. In fact, it is not unusual to find mixtures of both because of the fabricators decision to shop-bolt and field-weld, or vice versa. Welding, however, has much to offer in simplifying details and saving weight, as illustrated in Fig. 7.17e, Æ’, and g. The last represents the ultimate efficiency with respect to weight saving, and furthermore, it eliminates interfering details.
Deep wing brackets (Fig. 7.17h and i) are sometimes used for wall beams and spandrels designed to take wind stresses. Such deep brackets are, of course, acceptable for interior beam bracing whenever the brackets do not interfere with required clearances.
Not all beams need to wind-braced in tall buildings. Usually the wind load is concentrated on certain column lines, called bents, and the forces are carried through the bents to the ground. For example, in a wing of a building, it is possible to concentrate the wind load on the outermost bent. To do so may require a stiff floor or diaphragm-like system capable of distributing the wind loads laterally. Onehalf these loads may be transmitted to the outer bent, and one-half to the main building to which the wing connects.
Braced bents are invariably necessary across the narrow dimension of a building.
The question arises as to the amount of bracing required in the long dimension, since wind of equal unit intensity is assumed to act on all exposed faces of structures.
In buildings of square or near square proportions, it is likely that braced bents will be provided in both directions. In buildings having a relatively long dimension, as compared with width, the need for bracing diminishes. In fact, in many instances, wind loads are distributed over so many columns that the inherent rigidity of the whole system is sufficient to preclude the necessity of additional bracing. Column-to-column joints are treated differently for wind loads. Columns are compression members and transmit their loads, from section above to section below, by direct bearing between finished ends. It is not likely, in the average building, for the tensile stresses induced by wind loads ever to exceed the compressive pressure due to dead loads. Consequently, there is no theoretical need for bracing a column joint. Actually, however, column joints are connected together with nominal splice plates for practical considerations to tie the columns during erection and to obtain vertical alignment.
This does not mean that designers may always ignore the adequacy of column splices. In lightly loaded structures, or in exceptionally tall but narrow buildings, it is possible for the horizontal wind forces to cause a net uplift in the windward column because of the overturning action. The commonly used column splices should then be checked for their capacity to resist the maximum net tensile stresses caused in the column flanges. This computation and possible heaving up of the splice material may not be thought of as bracing; yet, in principle, the column joint is being wind-braced in a manner similar to the wind-braced floor-beam connections.
Shear Walls
Masonary walls enveloping a steel frame, interior masonry walls, and perhaps some stiff partitions can resist a substantial amount of lateral load. Rigid floor systems participate in lateral-force distribution by distributing the shears induced at each floor level to the columns and walls. Yet, it is common design practice to carry wind loads on the steel frame, little or no credit being given to the substantial resistance rendered by the floors and walls. In the past, some engineers deviated from this conversatism by assigning a portion of the wind loads to the floors and walls; nevertheless, the steel frame carried the major share. When walls of glass or thin metallic curtain walls, lightweight floors, and removable partitions are used, this construction imposes on the steel frame almost complete responsibility for transmittal of wind loads to the ground. Consequently, windbracing is critical for tall steel structures.
In tall, slender buildings, such as hotels and apartments with partitions, the cracking of rigid-type partitions is related to the wracking action of the frame caused by excessive deflection. One remedy that may be used for exceptionally slender frames (those most likely to deflect excessively) is to supplement the normal bracing of the steel frame with shear walls. Acting as vertical cantilevers in resisting lateral forces, these walls, often constructed of reinforced concrete, may be arranged much like structural shapes, such as plates, channels, Ts, Is, or Hs. (See also Arts. 3.2.4 and 5.12.) Walls needed for fire towers, elevator shafts, divisional walls, etc., may be extended and reinforced to serve as shear walls, and may relieve the steel frame of cumbersome bracing or avoid uneconomical proportions.
Bracing Industrial-Type Buildings
Bracing of low industrial buildings for horizontal forces presents fewer difficulties than bracing of multistory buildings, because the designer usually is virtually free to select the most efficient bracing without regard to architectural considerations or interferences. For this reason, conventional X bracing is widely used but not exclusively. Knee braces, struts, and sway frames are used where needed.
Wind forces acting on the frame shown in Fig. 7.18a, with hinged joints at the top and bottom of supporting columns, would cause collapse as indicated in Fig. 7.18b. In practice, the joints would not be hinged. However, a minimum- type connection at the truss connection and a conventional column base with anchor bolts located on the axis transverse to the frame would approximate this theoretical consideration of hinged joints. Therefore, the structure requires bracing capable of preventing collapse or unacceptable deflection.
In the usual case, the connection between truss and columns will be stiffened by means of knee braces (Fig. 7.18c). The rigidity so obtained may be supplemented by providing partial rigidity at the column base by simply locating the anchor bolts in the plane of the bent.
In buildings containing overhead cranes, the knee braced may interfere with crane operation. Then, the interference may be eliminated by fully anchoring the column base so that the column may function as a vertical cantilever (Fig. 7.18d).
The method often used for very heavy industrial buildings is to obtain substantial rigidity at both ends of the column so that the behavior under lateral load will resemble the condition illustrated in Fig. 7.18e. In both (d) and (e), the footings must be designed for such moments.
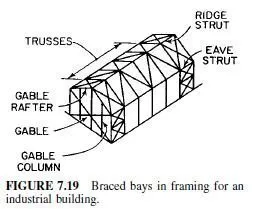 A common assumption in wind distribution for the type of light mill building shown in Fig. 7.19 is that the windward columns take a large share of the load acting on the side of the building and deliver the load directly to the ground. The remaining wind load on the side is delivered by the same columns to the roof systems, where the load joins with the wind forces imposed directly on the roof surface. Then, by means of diagonal X bracing, working in conjunction with the struts and top chords of the trusses, the load is carried to the eave struts, thence to the gables and, through diagonal bracing, to the foundations.
A common assumption in wind distribution for the type of light mill building shown in Fig. 7.19 is that the windward columns take a large share of the load acting on the side of the building and deliver the load directly to the ground. The remaining wind load on the side is delivered by the same columns to the roof systems, where the load joins with the wind forces imposed directly on the roof surface. Then, by means of diagonal X bracing, working in conjunction with the struts and top chords of the trusses, the load is carried to the eave struts, thence to the gables and, through diagonal bracing, to the foundations.
Because wind may blow from any direction, the building also must be braced for the wind load on the gables. This bracing becomes less important as the building increases in length and conceivably could be omitted in exceptionally long structures.
The stress path is not unlike that assumed for the transverse wind forces. The load generated on the ends is picked up by the roof system and side framing, delivered to the eave struts, and then transmitted by the diagonals in the end sidewall bays to the foundation.
No distribution rule for bracing is intended in this discussion; bracing can be designed many different ways. Whereas the foregoing method would be sufficient for a small building, a more elaborate treatment may be required for larger structures.
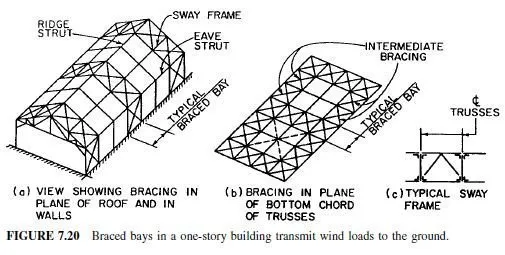
Braced bays, or towers, are usually favored for structures such as that shown in Fig. 7.20. There, a pair of transverse bents are connected together with X bracing in the plane of the columns, plane of truss bottom chords, plane of truss top chords, and by means of struts and sway frames. It is assumed that each such tower can carry the wind load from adjacent bents, the number depending on assumed rigid ities, size, span, and also on sound judgment. Usually every third or fourth bent should become a braced bay. Participation of bents adjoining the braced bay can be assured by insertion of bracing designated intermediate in Fig. 7.20b. This bracing is of greater importance when knee braces between trusses and columns cannot be used. When maximum lateral stiffness of intermediate bents is desired, it can be obtained by extending the X bracing across the span; this is shown with broken lines in Fig. 7.20b.
Buildings with flat or low-pitched roofs, shown in Fig. 7.12d and e, require little bracing because the trusses are framed into the columns. These columns are designed for the heavy moments induced by wind pressure against the building side.
The bracing that would be provided, at most, would consist of X bracing in the plane of the bottom chords for purpose of alignment during erection and a line or two of sway frames for longitudinal rigidity. Alignment bracing is left in the structure since it affords a secondary system for distributing wind loads.
Bracing Craneway Structures
All building framing affected by overhead cranes should be braced for the thrusts induced by sidesway and longitudinal motions of the cranes. Bracing used for wind or erection may be assumed to sustain the lateral crane loadings. These forces are usually concentrated on one bent. Therefore, normal good practice dictates that adjoining bents share in the distribution. Most effective is a system of X bracing located in the plane of the bottom chords of the roof trusses.
In addition, the bottom chords should be investigated for possible compression, although the chords normally are tension members. A heavily loaded crane is apt to draw the columns together, conceivably exerting a greater compression stress than the tension stress obtainable under dead load alone. This may indicate the need for intermediate bracing of the bottom chord.
Bracing Rigid Frames
Rigid frames of the type shown in Fig. 7.14 have enjoyed popular usage for gymnasiums, auditoriums, mess halls, and with increasing frequency, industrial buildings.
The stiff knees at the junction of the column with the rafter imparts excellent transverse rigidity. Each bent is capable of delivering its share of wind load directly to the footings. Nevertheless, some bracing is advisable, particularly for resisting wind loads against the end of the building. Most designers emphasize the importance of an adequate eave strut; it usually is arranged so as to brace the inside flange (compression) of the frame knee, the connection being located at the midpoint of the transition between column and rafter segments of the frame. Intermediate X bracing in the plane of the rafters usually is omitted.