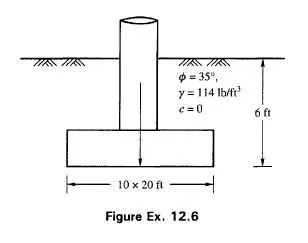
A rigid retaining wall 5 m high supports a backfill of cohesionless soil with 0= 30°. The water table is below the base of the wall. The backfill is dry and has a unit weight of 18 kN/m3. Determine Rankine’s passive earth pressure per meter length of the wall (Fig. Ex. 11.5).
Solution