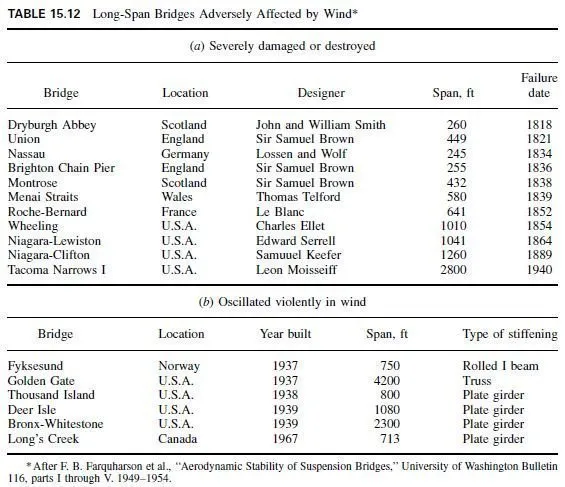
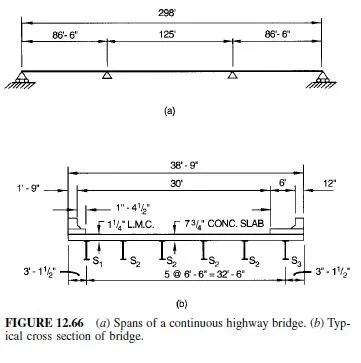
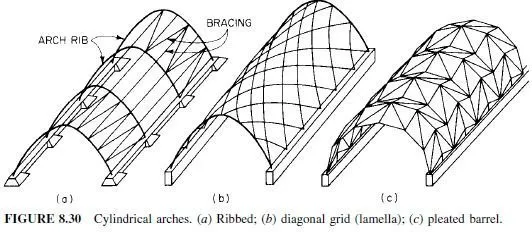
In addition to normal stresses (Art. 3.16), beams are subjected to shearing. Shear stresses vary over the cross section of a beam. At every point in the section, there are both a vertical and a horizontal shear stress, equal in magnitude [Eq. (3.37)].