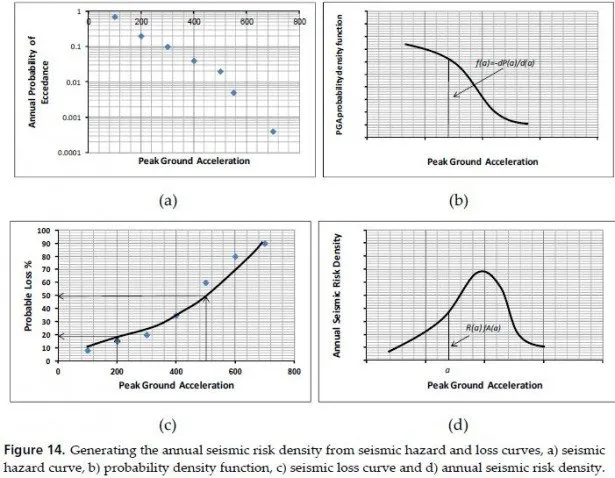
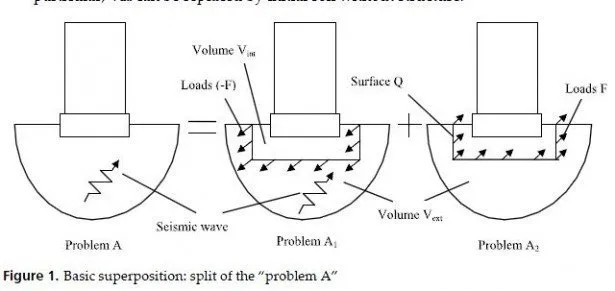
In direct method there always exists certain volume Vint. Usually the lower boundary (i.e., the bottom of Vint) is placed on the rock. In this case we presume that the additional waves radiating from the structure cannot change the motion of this boundary, as compared to the seismic field U0. As a consequence, we can substitute boundary conditions in problem A2, fixing the motion of the bottom (and obtaining it from problem B) instead of modeling Vext and applying loads F at surface Q. This substitution of the boundary conditions is shown in Fig.3.
One should remember that such substitution is accurate for rigid rock only. Otherwise, an error occurs due to the reflection of the additional waves from such a boundary back into Vint. This error can be significant. The example will be shown below.
After the lower boundary is fixed, lateral boundaries (usually vertical) remain to be set. In 1970s, when direct method was popular, there was an evolution of these boundaries from elementary ones (fixed or free) towards more accurate ones. The first important step was so-called acoustic boundaries by Lysmer and Kuhlemeyer [13,14].
Physical base is as follows. 1D elastic (without material damping!) massive rod with shear or pressure waves can be cut in two, and one half of it can be accurately replaced by viscous dashpot. This is illustrated by Fig. 4.
Dashpot viscosity parameter is a product of mass density Ï and wave velocity c. So, Lysmer and Kuhlemeyer suggested to place distributed shear and pressure dashpots over vertical lateral boundary (three dashpots along three axes in each node). Practically they substituted the half-infinite layer in Fig.3 by number of horizontal 1D rods normal to the boundary.
This boundary was far better than any elementary (fixed or free) boundary before.
Horizontal body waves normal to the boundary did not have artificial reflection into Vint (that is why this boundary was called non-reflecting boundary). This boundary could work in the time domain. Besides, this boundary was local: the response force acting to the node depended on the velocities of this node only, not neighbors.
This boundary was implemented in code LUSH [15], named after the authors (Lysmer, Udaka, Seed, Hwang). However, soon it turned out that the most important waves, radiating by structure in the soil underlain by rock are not horizontal body waves, but surface waves (see below). So, the artificial reflection at the boundary was not completely eliminated, and such a boundary could be placed only apart from the structure (3-4 plan sizes from the basements) to get more or less reasonable results.
One should keep in mind the important limitation: when wave process in Vint is modeled by ordinary finite elements, the element size should be about 1/8 (1/5 at most [1]) of the wavelength. It means that one cannot increase the finite element size going away from the structure (as they often do in statics). So, the increase in Vint leads to the considerable increase in the problem size and to the computational problems.
The next step was done by G.Waas [8,16,17]. Instead of replacing the infinite soil by number of horizontal rods he suggested to use homogeneous solutions i.e. the waves in the horizontally-layered medium underlain by rigid rock. These waves can be evaluated in the frequency domain only. According to G.Waas, in 2D case each homogeneous displacement varies in the horizontal direction following complex exponential rule with a certain complex frequency-dependent wave number; in the vertical direction it varies according to the finite-element interpolation. Later it turned out that in 3D case cylindrical waves in Vext along horizontal radius followed not exponents, but certain special Hankel functions with the same complex wave numbers as previously exponents in 2D case.
Any displacement of the lateral boundary (in the finite-element approximation) can be split into the sum of such waves in Vext. Then stresses are calculated at the boundary and finally nodal forces impacting Vint from Vext in response to boundary displacement can be evaluated. So, the final format of the Waas boundary was the dynamic stiffness matrix in the frequency domain, replacing Vext in the model. Unlike previous boundaries, this boundary was not local: response forces from Vext in the node depended not only on the motion of this very node, but on the motion of all the nodes. Thus, dynamic stiffness matrix became fully populated.
New boundaries (they were called transmitting boundaries) proved to be far more accurate than previous ones. They could be placed right near the basement, decreasing Vint and accelerating the analysis. So, LUSH was converted into FLUSH (=Fast LUSH) [18] for 2D problems. Then appeared code ALUSH (=Axisymmetric LUSH) [19] to solve 3D problems with axisymmetric geometry. However, there remained two important limitations: hard rock at the bottom and axisymmetric geometry of structure in 3D case. The next step forward was again done by J.Lysmer in EERC. But this new approach will be discussed later (see combined method).