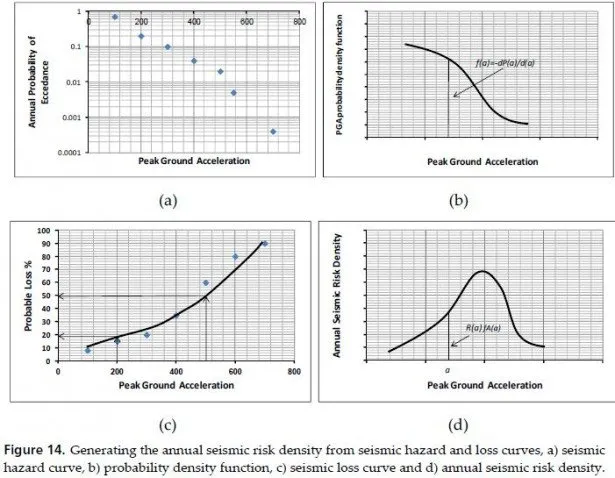
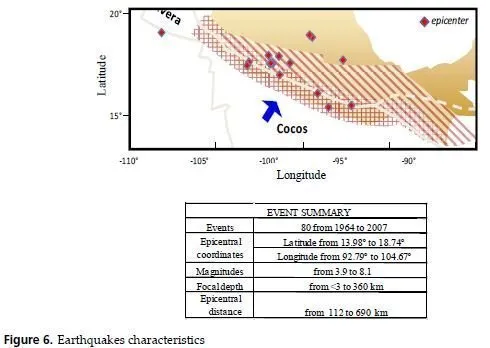
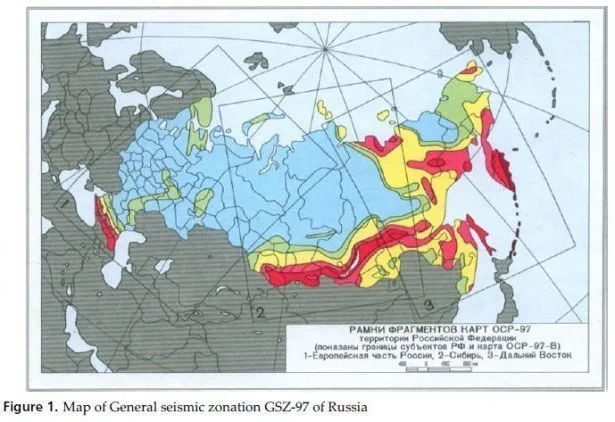
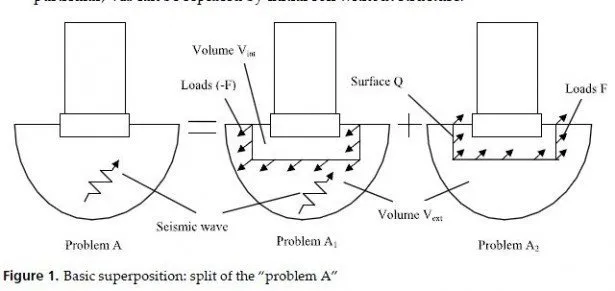
As it was shown above, the components of SC complement each other, rather than compete.
It becomes clear that FL, NC and GA are more effective when used in combinations. Lack of interpretability of neural networks and poor learning capability of fuzzy systems are similar problems that limit the application of these tools. Neurofuzzy systems are hybrid systems which try to solve this problem by combining the learning capability of connectionist models with the interpretability property of fuzzy systems. As it was noted above, in case of dynamic work environment, the automatic knowledge base correction in fuzzy systems becomes necessary. On the other hand, artificial neural networks are successfully used in problems connected to knowledge acquisition using learning by examples with the required degree of precision.
Incorporating neural networks in fuzzy systems for fuzzification, construction of fuzzy rules, optimization and adaptation of fuzzy knowledge base and implementation of fuzzy reasoning is the essence of the Neurofuzzy approach.
The combination of genetic algorithms with neural networks yields promising results as
well. It is known that one of main problems in development of artificial neural systems is selection of a suitable learning method for tuning the parameters of a neural network (weights, thresholds, and structure). The most known algorithm is the “error back propagation” algorithm. Unfortunately, there are some difficulties with “back propagation”. First, the effectiveness of the learning considerably depends on initial set of weights, which are generated randomly. Second, the “back propagation”, like any other gradient-based method, does not avoid local minima. Third, if the learning rate is too slow, it requires too much time to find the solution. If, on the other hand, the learning rate is too high it can generate oscillations around the desired point in the weight space.
Fourth, “back propagation” requires the activation functions to be differentiable. This condition does not hold for many types of neural networks. Genetic algorithms used for solving many optimization problems when the “strong” methods fail to find appropriate solution, can be successfully applied for learning neural networks, because they are free of the above drawbacks.
The models of artificial neurons, which use linear, threshold, sigmoidal and other transfer functions, are effective for neural computing. However, it should be noted that such models are very simplified. For example, reaction of a biological axon is chaotic even if the input is periodical. In this aspect the more adequate model of neurons seems to be chaotic. Model of a chaotic neuron can be used as an element of chaotic neural networks. The more adequate results can be obtained if using fuzzy chaotic neural networks, which are closer to biological computation. Fuzzy systems with If-Then rules can model non-linear dynamic systems and capture chaotic attractors easily and accurately. Combination of Fuzzy Logic and Chaos Theory gives us useful tool for building system’s chaotic behavior into rule structure.
Identification of chaos allows us to determine predicting strategies. If we use a Neural Network Predictor for predicting the system’s behavior, the parameters of the strange attractor (in particular fractal dimension) tell us how much data are necessary to train the neural network. The combination of Neurocomputing and Chaotic computing technologies can be very helpful for prediction and control.
The cooperation between these formalisms gives a useful tool for modeling and reasoning under uncertainty in complicated real-world problems. Such cooperation is of particular importance for constructing perception-based intelligent information systems. We hope that the mentioned intelligent combinations will develop further, and the new ones will be proposed. These SC paradigms will form the basis for creation and development of Computational Intelligence.