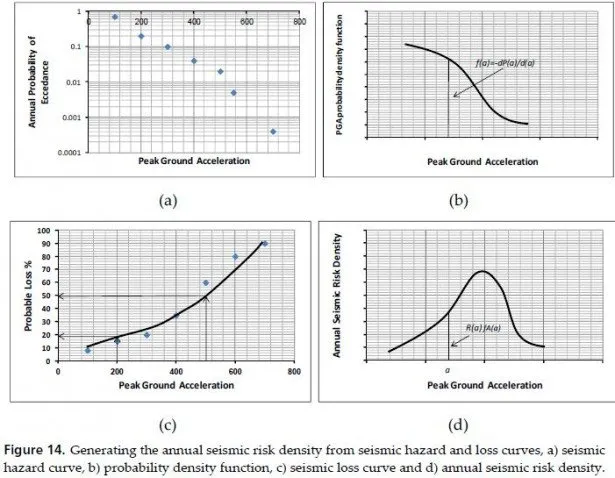
The embankment ranking and prioritization procedures in the seismic vulnerability methodology are based on three parameters that have to be derived for each embankment.
They are the seismic slope stability C/D ratio, anticipated embankment displacement, and liquefaction potential at the embankment site. The way by which each parameter is calculated is described in the following sub-sections. After calculating the three ranking parameters, categorization of the embankment behavior during a specified seismic event is carried out using Table 2.
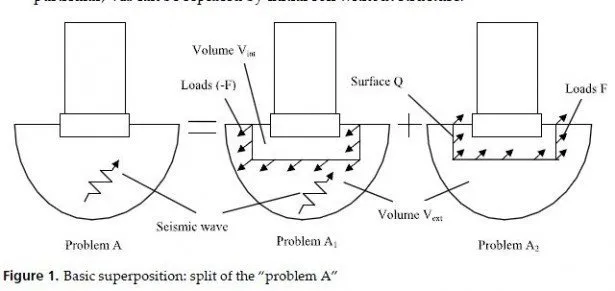
Capacity/Demand (C/D) Ratio: The seismic slope stability C/D ratio of a bridge embankment is calculated for two possible failure types, known as circular base failure and wedge type failure. For a circular base failure that is shown in Figure 2a, the factor of safety (FScb) is calculated from Eq. 1.


where FScb is the factor of safety against circular base failure, S1 is the un-drained shear strength of the soil beneath the embankment, H is the embankment height (Figure 1), and γ1 is the density of the soil layer (Table 1). The parameters R1, R2, D1, and D2 are obtained from Equations (2), (3), (4), and (5), respectively.

where λ is the ratio of S2/S1, S2 is the embankment soil un-drained shear strength and γ2 is the embankment soil density (Table 1). For the values of x and r that result in the lowest factor of safety, designated xc and rc, the term in brackets of Eq. 1 has to be calculated and is called the stability number for the designated slope. The use of Eq. 1 in a spreadsheet with an optimization function provides reliable estimates of these parameters over the designated slope inclinations. Specifically, the Solver® function in Microsoft Excel XP® can be utilized to find rc and xc in order to minimize the factor of safety. By using pseudo-static analysis, assuming FScb = 1.0 in Eq. 1, and optimizing for rc and xc the horizontal earthquake acceleration factor (khf) is obtained for different assumed elevations of the upper level of the bedrock layer. The critical Khf causing a circular base failure is obtained from Eq. 6.

Although a base failure predominates for the slope geometry typically encountered in highway embankments, a wedge failure extending upward from the toe of the embankment may be more critical for steeper slopes. The wedge type failure geometry is depicted in Figure 2b. For a wedge type failure, the factor of safety (FSw) is obtained from Eq. 7.
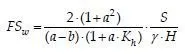
where FSw is the factor of safety against embankment wedge failure; S is selected as the estimated shear strength along the base of the failure wedge and the parameter a; shown in Figure 2b, is the parameter to be optimized. The horizontal earthquake acceleration factor (khfw) shall be obtained for different assumed elevations of the upper level of the bedrock layer by using pseudo-static analysis, assuming FSw = 1.0 in Eq. 7, and optimizing by changing the parameter a. The critical Khfw causing a wedge type failure of the embankment is obtained from Eq. 8.

The lesser factor of safety for a circular base failure (FScb) and for a wedge type failure (FSw) is then called the capacity/demand (C/D) ratio for the designated elevation of the upper level of the bedrock layer. Similar processes are followed for other elevations of the upper level of the bedrock layer in order to obtain the overall least C/D ratio, which is called the minimum capacity/demand ratio, (C/D)min.. The considered horizontal earthquake acceleration (Khf) is the one that corresponds to the (C/D)min. from all of the failure cases.
Embankment Displacement: For an embankment with C/Dmin.1.0, it is important to estimate how far the mass actually displaces during the seismic event. This is carried out by calculating the anticipated embankment displacement (u). For a designated embankment, the PGA is identified for a specified seismic event; this parameter is also known as the maximum acceleration (Amax.). For the embankment to displace, the maximum acceleration has to exceed the acceleration causing embankment yielding. Assuming that the yield acceleration is equal to the Khf, that corresponds to the (C/D)min. from all the failure cases, the yield factor (Y) is estimated as the ratio of Ay/Amax, where Ay is the yield acceleration, and Amax. equals to the PGA. By utilizing the site geometry and the specified sub-surface conditions, it is possible to use a simple model to determine the approximate yield acceleration of a bridge embankment. A sliding block solution can then be applied to estimate the displacement of the slope for a specified PGA, exceeding Ay. As Y decreases, u increases correspondingly. For Y1.0, embankment displacement is likely to occur. The displacement (u) can be estimated by the use of Eq. 9 [6].
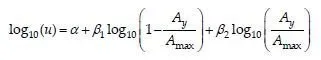
where u is the displacement, in centimeters; ï¡, ï¢1, ï¢2 are the bedrock coefficients that are required to calculate the embankment displacement. Dodds [8] reported the way by which the bedrock coefficients are calculated for both bedrock and soil sites based on the potential earthquake magnitude at the geographic location of the bridge site. The value of ï¡ for both bedrock and soil can be obtained by use of Eq. 10a and Eq. 10b. The parameter, ï¢1, can be calculated for both the bedrock and soil by the use of Eq. 11a and Eq. 11b, while ï¢2 can be calculated by the use of Eq. 12a and Eq. 12b.

where Mb,Lg is the body-wave magnitude of the anticipated earthquake. As the seismic slope stability of an embankment decreases, a larger displacement is expected, providing a stronger indication of an at-risk embankment than that obtained from the (C/D)min. ratio. The analysis using this method eliminates the misleading condition of how to assess an embankment with (C/D)min. ratio1.0. Instead, this method forces a consideration of the possible displacement that may be observed, a better prediction of the actual behavior of a given embankment during a seismic event.
Liquefaction Potential: The mechanical behavior, which includes the liquefaction potential during the seismic event, is another important parameter in the seismic vulnerability assessment and prioritization of bridge embankments. Cohesion-less soils, such as alluvium and sandy/gravelly continental deposits are susceptible to liquefaction, and alluvium is the most likely to experience liquefaction. Where the boring logs data is available, straightforward steps are followed to define the liquefaction potential as reported by [9]. In order to overcome the difficulties encountered when such data is not available, an alternate approach to define the liquefaction potential is followed. The liquefaction potential has to be assessed in accordance with the following two sub-sections Boring Logs Are Not Available: Where the boring log data of each embankment site is not available, the liquefaction potential can be addressed based on the Seismic Retrofit Manual for Highway Bridges [1]. The susceptibility of the embankment soil to liquefaction is classified as one of three possible types (Table 3).

The three liquefaction possibilities are: high susceptibility, moderate susceptibility, and low susceptibility. High susceptibility is associated with saturated loose sands, saturated silty sands, or non-plastic sands. A bridge that crosses a waterway where soils have been deposited over long periods of time by flowing water is often constructed on loose saturated cohesion-less deposits that are the most susceptible to liquefaction. Moderate susceptibility is associated with medium dense soils such as compacted sand soils. Low susceptibility is associated with dense soils.
Boring Logs Are Available: Where the boring log data is available, the liquefaction potential at the bridge site is determined by the method reported by [9]. To determine a reasonably accurate value of the cyclic stress ratio causing liquefaction and induced by the earthquake motion, a correlation between the liquefaction characteristics and standard penetration test (SPT) blow-count values (N values), described by [10] is used. The average cyclic shear induced by the seismic event is obtained from Eq. 13.

where Ï„h,avg is the average cyclic shear stress during the time history of interest, σ’o is the effective overburden stress at any depth, Amax is the maximum earthquake ground surface acceleration, and rd is a stress reduction correction factor. The mean effective and total stresses (σ’o and σ’o) are replaced with the effective and total vertical stresses. The stress reduction factor (rd), defined by [10], is computed using the depth (z) in meters as shown in
Eq. 14.
![]()
The soil penetration resistance is the corrected normalized standard penetration resistance, N1,60, which is defined by [10] and [5] in Eq. 15.
![]()
Where CN is the correction coefficient, ERm is rod energy ratio, and Nm is the measured SPT blow-count per foot. With the determination of both the cyclic stress ratio induced during the earthquake and the cyclic stress ratio required to cause liquefaction, the factor of safety against liquefaction (FSl) is calculated as shown in Eq. 16.