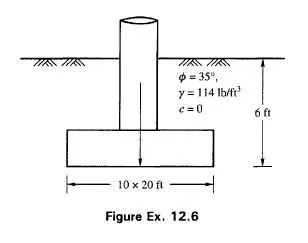
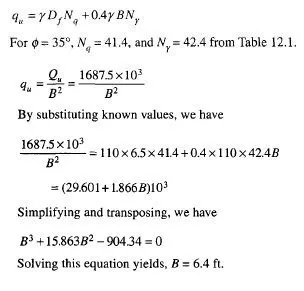There are occasions where structures are required to be built on slopes or near the edges of slopes. Since full formations of shear zones under ultimate loading conditions are not possible on the sides close to the slopes or edges, the supporting capacity of soil on that side get considerably reduced.
Meyerhof (1957) extended his theories to include the effect of slopes on the stability of foundations. Figure 12.19 shows a section of a foundation with the failure surfaces under ultimate loading condition. The stability of the foundation depends on the distance b of the top edge of the slope from the face of the foundation.
The form of ultimate bearing capacity equation for a strip footing may be expressed as (Meyerhof, 1957)
![]()
The upper limit of the bearing capacity of a foundation in a purely cohesive soil may be estimated from
![]()
The resultant bearing capacity factors Ncq and N depend on the distance b, ß @ and the DJB ratio. These bearing capacity factors are given in Figs 12.20 and 12.21 for strip foundation in purely cohesive and cohesionless soils respectively. It can be seen from the figures that the bearing capacity factors increase with an increase of the distance b Beyond a distance of about 2 to 6 times the foundation width B, the bearing capacity is independent of the inclination of the slope, and becomes the same as that of a foundation on an extensive horizontal surface.
For a surcharge over the entire horizontal top surface of a slope, a solution of the slope??stability has been obtained on the basis of dimensionless parameters called the stability number Ns, expressed as
![]()
The bearing capacity of a foundation on purely cohesive soil of great depth can be represented by Eq. (12.67) where the Nc factor depends on b as well as ß, and the stability number N. This bearing capacity factor, which is given in the lower parts of Fig. 12.20, decrease considerably with greater height and to a smaller extent with the inclination of the slope. For a given height and slope angle, the bearing capacity factor increases with an increase in b. and
beyond a distance of about 2 to 4 times the height of the slope, the bearing capacity is independent of the slope angle. Figure 12.20 shows that the bearing capacity of foundations on top of a slope is governed by foundation failure for small slope height (A^ approaching infinity) and by overall slope failure for greater heights.
The influence of ground water and tension cracks (in purely cohesive soils) should also be taken into account in the study of the overall stability of the foundation.
Meyerhof (1957) has not supported his theory with any practical examples of failure as any published data were not available for this purpose.