Concept of Coulomb’s Formula
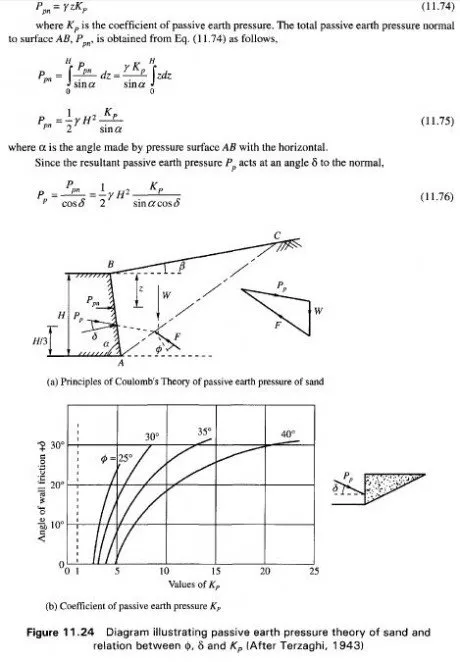
Coulomb (1776) computed the passive earth pressure of ideal sand on the simplifying assumption that the entire surface of sliding consists of a plane through the lower edge A of contact face AB as shown in Fig. 1 1.24a. Line AC represents an arbitrary plane section through this lower edge. The forces acting on this wedge and the polygon of forces are shown in the figure. The basic equation for computing the passive earth pressure coefficient may be developed as follows:
Consider a point on pressure surface AB at a depth z from point B (Fig 11.24a). The normal component of the earth pressure per unit area of surface AB may be expressed by the equation,
Passive Earth Pressure Coefficient
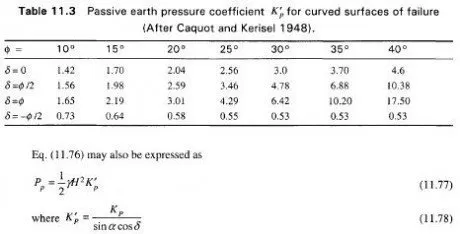
Coulomb developed an analytical solution for determining Kp based on a plane surface of failure and this is given in Eq. (11.57). Figure 11.24(b) gives curves for obtaining Coulomb’s values of Kp for various values of 8 and 0 for plane surfaces of failure with a horizontal backfill. They indicate that for a given value of 0 the value of Kp increases rapidly with increasing values of 8. The limitations of plane surfaces of failure are given in Section 11.9. Curved surfaces of failure are normally used for computing P or Kp when the angle of wall friction 8 exceeds 0/3. Experience indicates that the curved surface of failure may be taken either as a part of a logarithmic spiral or a circular arc. Caquot and Kerisel (1948) computed K’p by making use of curved surfaces of failure for various values of 0, 8, 0 and /3. Caquot and Kerisel’s calculations for determining K’p for curved surfaces of failure are available in the form of graphs.
Table 11.3 gives the values of K’pfor various values of 0 and 8 for a vertical wall with a horizontal backfill (after Caquot and Kerisel, 1948).
In the vast majority of practical cases the angle of wall friction has a positive sign, that is, the wall transmits to a soil a downward shearing force. The negative angle of wall friction might develop in the case of positive batter piles subjected to lateral loads, and also in the case of pier foundations for bridges subjected to lateral loads.