Coulomb made the following assumptions in the development of his theory:
1. The soil is isotropic and homogeneous
2. The rupture surface is a plane surface
3. The failure wedge is a rigid body
4. The pressure surface is a plane surface
5. There is wall friction on the pressure surface
6. Failure is two-dimensional and
7. The soil is cohesionless
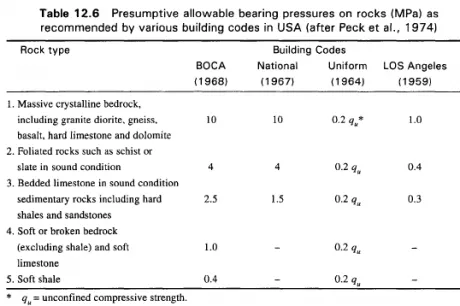
Consider Fig. 11.17.
1. AB is the pressure face
2. The backfill surface BE is a plane inclined at an angle /3 with the horizontal
3. a is the angle made by the pressure face AB with the horizontal
4. H is the height of the wall
5. AC is the assumed rupture plane surface, and
6. 6 is the angle made by the surface AC with the horizontal
If AC in Fig. 17(a) is the probable rupture plane, the weight of the wedge W length of the wall may be written as
W = yA, where A = area of wedge ABC

The various forces that are acting on the wedge are shown in Fig. 11.17(a). As the pressure face AB moves away from the backfill, there will be sliding of the soil mass along the wall from B towards A. The sliding of the soil mass is resisted by the friction of the surface. The direction of the shear stress is in the direction from A towards B. lfPn is the total normal reaction of the soil pressure acting on face AB, the resultant of Pn and the shearing stress is the active pressure Pa making an angle 8 with the normal. Since the shearing stress acts upwards, the resulting Pa dips below the normal. The angle 5 for this condition is considered positive. As the wedge ABC ruptures along plane AC, it slides along this plane. This is resisted by the frictional force acting between the soil at rest below AC, and the sliding wedge. The resisting shearing stress is acting in the direction from A towards C. If Wn is the normal component of the weight of wedge W on plane AC, the resultant of the normal Wn and the shearing stress is the reaction R. This makes an angle 0 with the normal since the rupture takes place within the soil itself. Statical equilibrium requires that the three forces Pa, W, and R meet at a point. Since AC is not the actual rupture plane, the three forces do not meet at a point. But if the actual surface of failure AC’C is considered, all three forces meet at a point. However, the error due to the nonconcurrence of the forces is very insignificant and as such may be neglected. The polygon of forces is shown in Fig. 11.17(b). From the polygon of forces, we may write

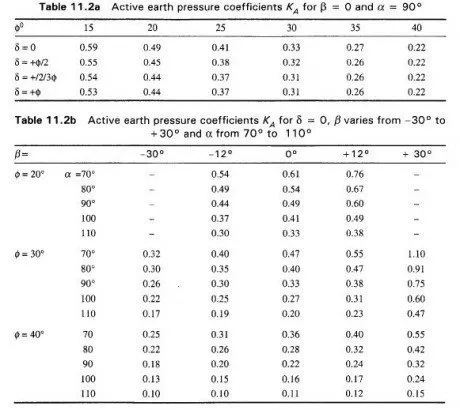
where KA is the active earth pressure coefficient.