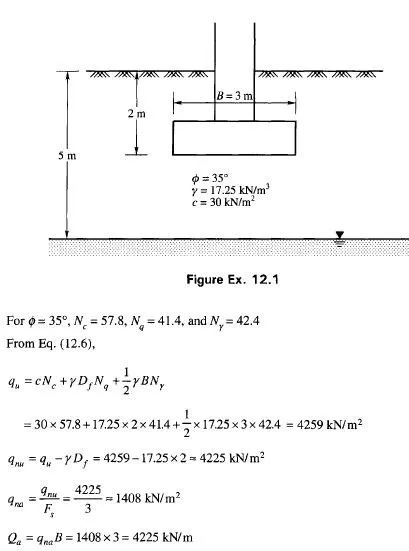
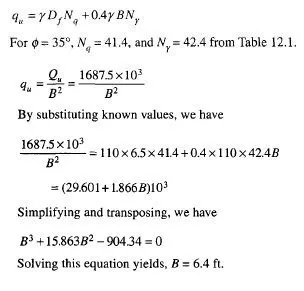The relationship between deflection, y, at any point on an elastic beam and the corresponding bending moment M may be expressed by the equation
![]()
The equations for shear V and reaction q at the same point may be expressed as

where x is the coordinate along the length of the beam.
From the basic assumption of an elastic foundation

The classical solutions of Eq. (14.13) being of closed form, are not general in their application. Hetenyi (1946) developed equations for a load at any point along a beam. The development of solutions is based on the concept that the beam lies on a bed of elastic springs which is based on Winkler’s hypothesis. As per this hypothesis, the reaction at any point on the beam depends only on the deflection at that point.
Methods are also available for solving the beam-problem on an elastic foundation by the
method of finite differences (Malter, 1958). The finite element method has been found to be the
most efficient of the methods for solving beam-elastic foundation problem. Computer programs are
available for solving the problem.
Since all the methods mentioned above are quite involved, they are not dealt with here. Interested readers may refer to Bowles (1996).