Ground motions during an earthquake tend to increase the earth pressure above the static earth pressure. Retaining walls with horizontal backfills designed with a factor of safety of 1.5 for static loading are expected to withstand horizontal accelerations up to 0.2g. For larger accelerations, and for walls with sloping backfill, additional allowances should be made for the earthquake forces. Murphy (1960) shows that when subjected to a horizontal acceleration at the base, failure occurs in the soil mass along a plane inclined at 35° from the horizontal . The analysis of Mononobe (1929) considers a soil wedge subjected to vertical and horizontal accelerations to behave as a rigid body sliding over a plane slip surface.
The current practice for earthquake design of retaining walls is generally based on design rules suggested by Seed and Whitman (1970). Richards et al. (1979) discuss the design and behavior of gravity retaining walls with unsaturated cohesionless backfill. Most of the papers make use of the popular Mononobe-Okabe equations as a starting point for their own analysis. They follow generally the pseudoplastic approach for solving the problem. Solutions are available for both the active and passive cases with as granular backfill materials. Though solutions for (c-0) soils have been presented by some investigators (Prakash and Saran, 1966, Saran and Prakash, 1968), their findings have not yet been confirmed, and as such the solutions for (c-0) soils have not been taken up in this chapter.
Earthquake Effect on Active Pressure with Granular Backfill
The Mononobe-Okabe method (1929, 1926) for dynamic lateral pressure on retaining walls is a straight forward extension of the Coulomb sliding wedge theory. The forces that act on a wedge under the active state are shown in Fig. 11.25
In Fig. 11.25 AC in the sliding surface of failure of wedge ABC having a weight W with inertial components kv W and khW. The equation for the total active thrust Pae acting on the wall AB under dynamic force conditions as per the analysis of Mononobe-Okabe is
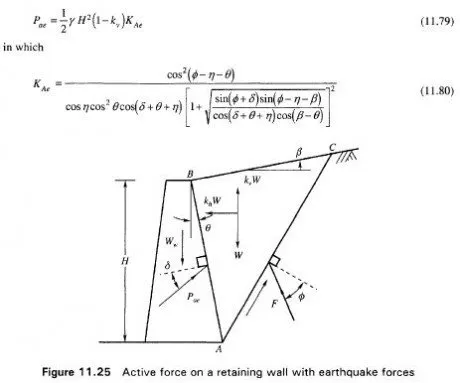

The dynamic component Pae is expected to act at a height 0.6H above the base whereas the static earth pressure acts at a height H/3. For all practical purposes it would be sufficient to assume that the resultant force Pae acts at a height H/2 above the base with a uniformly distributed pressure.

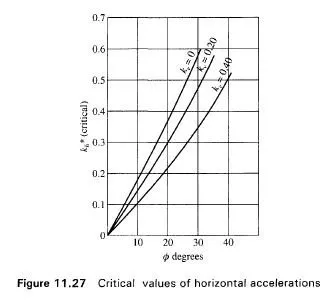
It has been shown that the active pressure is highly sensitive to both the backfill slope (3, and the friction angle 0 of the soil (Fig. 11.26).
It is necessary to recognize the significance of the expression