Lateral Pressures by Theory of Elasticity for Surcharge Loadson the Surface of Backfill

The surcharges on the surface of a backfill parallel to a retaining wall may be any one of the following
1. A concentrated load
2. A line load
3. A strip load

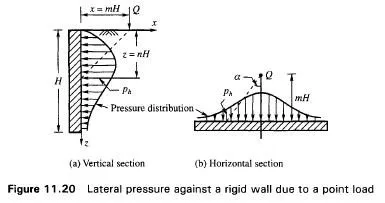
Lateral Pressure at a Point in a Semi-Infinite Mass due to a Concentrated Load on the Surface
Tests by Spangler (1938), and others indicate that lateral pressures on the surface of rigid walls can be computed for various types of surcharges by using modified forms of the theory of elasticity equations. Lateral pressure on an element in a semi-infinite mass at depth z from the surface may be calculated by Boussinesq theory for a concentrated load Q acting at a point on the surface. The equation may be expressed as (refer to Section 6.2 for notation)

Eq. (11.63) is strictly applicable for computing lateral pressures at a point in a semiinfinite mass. However, this equation has to be modified if a rigid wall intervenes and breaks the continuity of the soil mass. The modified forms are given below for various types of surcharge loads.
Lateral Pressure on a Rigid Wall Due to a Concentrated Load on the Surface Let Q be a point load acting on the surface as shown in Fig. 11.20. The various equations are

Lateral Pressure on a Rigid Wall due to Line Load
A concrete block wall conduit laid on the surface, or wide strip loads may be considered as a series of parallel line loads as shown in Fig. 11.21. The modified equations for computing ph are as follows:

 
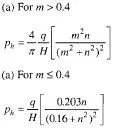
Lateral Pressure on a Rigid Wall due to Strip Load
A strip load is a load intensity with a finite width, such as a highway, railway line or earth
embankment which is parallel to the retaining structure. The application of load is as given in Fig.
11.22.
The equation for computing ph is