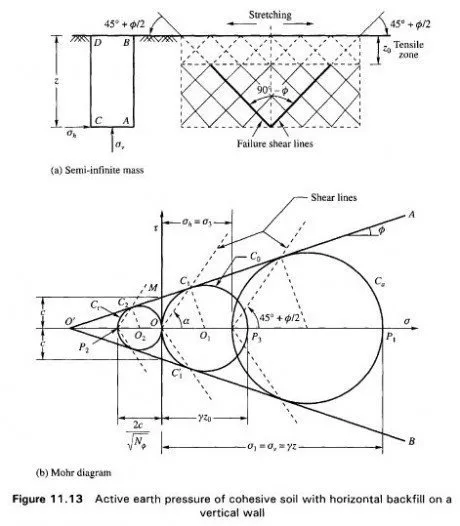
In Fig. 1 1.1 3(a) is shown a prismatic element in a semi-infinite mass with a horizontal surface. The vertical pressure on the base AD of the element at depth z is
![]()
The horizontal pressure on the element when the mass is in a state of plastic equilibrium may be determined by making use of Mohr’s stress diagram [Fig. 1 1.13(b)].
Mohr envelopes O’A and O’E for cohesive soils are expressed by Coulomb’s equation
![]()
Point Pj on the cr-axis represents the state of stress on the base of the prismatic element. When the mass is in the active state cr, is the major principal stress Cfj. The horizontal stress oh is the minor principal stress <73. The Mohr circle of stress Ca passing through P{ and tangential to the Mohr envelopes O’A and O’B represents the stress conditions in the active state. The relation between the two principal stresses may be expressed by the expression
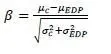

Equations (11 .32) and (1 1.33) indicate that the active pressure pa is tensile between depth 0 and ZQ. The Eqs. (1 1.32) and (1 1.33) can also be obtained from Mohr circles CQ and Ct respectively.
Shear Lines Pattern
The shear lines are shown in Fig. 1 1 . 13(a). Up to depth ZQ they are shown dotted to indicate that this zone is in tension.
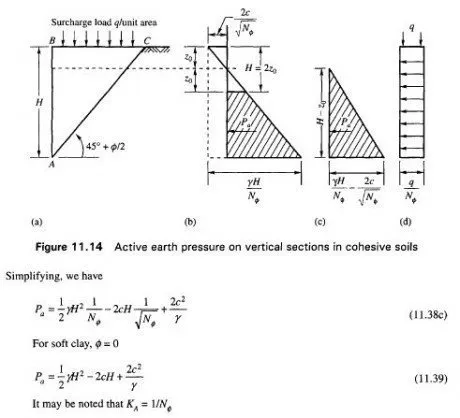
Total Active Earth Pressure on a Vertical Section
If AB is the vertical section [1 1.14(a)], the active pressure distribution against this section of height H is shown in Fig. 1 1.1 4(b) as per Eq. (1 1.30). The total pressure against the section is

Soil does not resist any tension and as such it is quite unlikely that the soil would adhere to the wall within the tension zone of depth z0 producing cracks in the soil. It is commonly assumed that the active earth pressure is represented by the shaded area in Fig. 1 1.14(c). The total pressure on wall AB is equal to the area of the triangle in Fig. 11.14(c) which is equal to