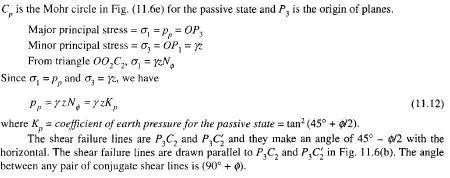Let AT in Fig. 11.6(a) represent the horizontal surface of a semi-infinite mass of cohesionless soil with a unit weight y. The soil is in an initial state of elastic equilibrium. Consider a prismatic block ABCD. The depth of the block is z and the cross-sectional area of the block is unity. Since the element is symmetrical with respect to a vertical plane, the normal stress on the base AD is

where KQ is the coefficient of earth pressure for the at rest condition which is assumed as a constant for a particular soil. The horizontal stress oh varies from zero at the ground surface to KQyz at depth z.
If we imagine that the entire mass is subjected to horizontal deformation, such deformation is a plane deformation. Every vertical section through the mass represents a plane of symmetry for the entire mass. Therefore, the shear stresses on vertical and horizontal sides of the prism are equal to zero.
Due to the stretching, the pressure on vertical sides AB and CD of the prism decreases until the conditions of plastic equilibrium are satisfied, while the pressure on the base AD remains unchanged. Any further stretching merely causes a plastic flow without changing the state of stress. The transition from the state of plastic equilibrium to the state of plastic flow represents the failure of the mass. Since the weight of the mass assists in producing an expansion in a horizontal direction, the subsequent failure is called active failure.
If, on the other hand, the mass of soil is compressed, as shown in Fig. 11.6(b), in a horizontal direction, the pressure on vertical sides AB and CD of the prism increases while the pressure on its base remains unchanged at yz. Since the lateral compression of the soil is resisted by the weight of the soil, the subsequent failure by plastic flow is called a passive failure.
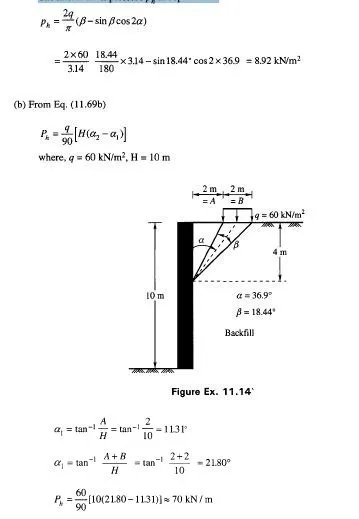
The problem now consists of determining the stresses associated with the states of plastic equilibrium in the semi-infinite mass and the orientation of the surface of sliding. The problem was solved by Rankine (1857).
The plastic states which are produced by stretching or by compressing a semi-infinite mass of soil parallel to its surface are called active and passive Rankine states respectively. The orientation of the planes may be found by Mohr’s diagram.
Horizontal stretching or compressing of a semi-infinite mass to develop a state of plastic equilibrium is only a concept. However, local states of plastic equilibrium in a soil mass can be created by rotating a retaining wall about its base either away from the backfill for an active state or into the backfill for a passive state in the way shown in Figs. 1 1.3(c) and (d) respectively. In both cases, the soil within wedge ABC will be in a state of plastic equilibrium and line AC represents the rupture plane.
Mohr Circle for Active and Passive States of Equilibrium in Granular Soils
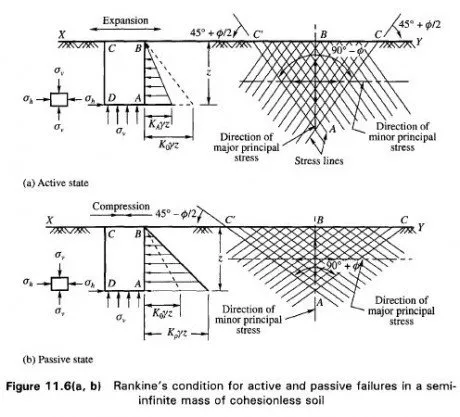
Point P{ on the d-axis in Fig. 1 1.6(e) represents the state of stress on base AD of prismatic element ABCD in Fig. 1 1.6(a). Since the shear stress on AD is zero, the vertical stress on the base

Two circles Ca and C can be drawn passing through Pl and at the same time tangential to the Mohr envelopes OA and OB. When the semi-infinite mass is stretched horizontally, the horizontal stress on vertical faces AB and CD (Fig. 1 1.6 a) at depth z is reduced to the minimum possible and this stress is less than vertical stress ov. Mohr circle Ca gives the state of stress on the prismatic element at depth z when the mass is in active failure. The intercepts OPl and OP2 are the major and minor principal stresses respectively.
When the semi-infinite mass is compressed (Fig. 1 1.6 b), the horizontal stress on the vertical face of the prismatic element reaches the maximum value OP3 and circle C is the Mohr circle which gives that state of stress.
Active State of Stress

Passive State of Stress