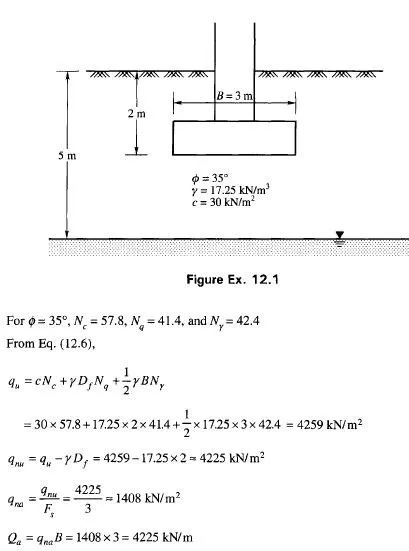
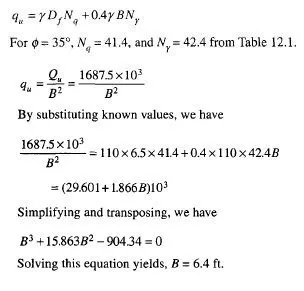The content:
1.1 Standard penetration tests (SPT)
1.1.1 Modification of raw SPT values
1.1.1.1 Method A
1.1.1.2 Method B
1.1.2 Relative density
1.1.3 Undrained soil strength vs. SPT N
1.1.4 Friction angle vs. SPT N, Dr, and Ip
1.1.5 Parameters affecting strength
1.2 Cone penetration tests
1.2.1 Undrained shear strength
1.2.2 SPT blow counts using qc
1.3 Soil stiffness
1.4 Stiffness and strength of rock
1.4.1 Strength of rock
1.4.2 Shear modulus of rock
Standard penetration tests (SPT)
The Standard Penetration Test was developed in the late 1920s, but the test procedure was not standardized until 1958 (see ASTM D1586), with periodic revisions to date. The test consists of the following procedures: (a) driving the standard split-barrel sampler a distance of 460 mm into the soil at the bottom of the boring, (b) counting the number of the blows to drive the sampler for the last two 150 mm distance (total = 305 mm) to obtain the blow counts number N, (c) using a 63.5-kg driving mass (or hammer) falling free from a height of 760 mm onto the top of the boring rods. The SPT test is normally halted if (a) 50 blows are required for any 150 mm increment, (b) 100 blows are obtained (to drive the required 300 mm), and (c) 10 successive blows produce no advance. The raw SPT data must be corrected to yield the real (corrected) value of SPT, as outlined next.