The coefficient of subgrade reaction is defined as the ratio between the pressure against the footing or mat and the settlement at a given point expressed as The coefficient of subgrade reaction is defined as the ratio between the pressure against the footing or mat and the settlement at a given point expressed as eq 14.2

1 . The value of k^ is independent of the magnitude of pressure.
2. The value of &s has the same value for every point on the surface of the footing.
Both the assumptions are strictly not accurate. The value of ks decreases with the increase of the magnitude of the pressure and it is not the same for every point of the surface of the footing as the settlement of a flexible footing varies from point to point. However the method is supposed to give realistic values for contact pressures and is suitable for beam or mat design when only a low order of settlement is required.
Factors Affecting the Value of ks
Terzaghi (1955) discussed the various factors that affect the value of ks. A brief description of his
arguments is given below.
Consider two foundation beams of widths Bl and B2 such that B2 = nB{ resting on a compressible subgrade and each loaded so that the pressure against the footing is uniform and equal
to q for both the beams (Fig. 14. Ib). Consider the same points on each beam and, let
y1 = settlement of beam of width B1
y2 = settlement of beam of width B2

where ks is the coefficient of subgrade reaction of a long footing of width B meters and resting on stiff clay; ksl is the coefficient of subgrade reaction of a long footing of width 0.30 m (approximately), resting on the same clay. It is to be noted here that the value of ksl is derived from ultimate settlement values, that is, after consolidation settlement is completed.
If the beams are resting on clean sand, the final settlement values are obtained almost instantaneously. Since the modulus of elasticity of sand increases with depth, the deformation characteristics of the sand change and become less compressible with depth. Because of this characteristic of sand, the lower portion of the bulb of pressure for beam B2 is less compressible than that of the sand enclosed in the bulb of pressure of beam Bl.
The settlement value y2 lies somewhere between yl and nyr It has been shown experimentally (Terzaghi and Peck, 1948) that the settlement, y, of a beam of width B resting on sand is given by the expression
![]()
where y{ = settlement of a beam of width 0.30 m and subjected to the same reactive pressure as the
beam of width B meters.
Hence, the coefficient of subgrade reaction ks of a beam of width B meters can be obtained from the following equation
![]()
where ks1 = coefficient of subgrade reaction of a beam of width 0.30 m resting on the same sand.
Measurement of ks1
A value for ks1 for a particular subgrade can be obtained by carrying out plate load tests. The standard size of plate used for this purpose is 0.30 x 0.30 m size. Let k1 be the subgrade reaction for a plate of size 0.30 x 0.30 rn size.
From experiments it has been found that ks1=k1 for sand subgrades, but for clays ksl varies
with the length of the beam. Terzaghi (1955) gives the following formula for clays

Procedure to Find ks
For sand
1. Determine k1 from plate load test or from estimation.
2. Since kss1 =~ k1 use Eq. (14.6) to determine ks for sand for any given width B meter.
For clay
1 . Determine k1 from plate load test or from estimation
2. Determine ks1, from Eq. (14.7a) as the length of beam is known.
3. Determine ks from Eq. (14.4) for the given width B meters.
When plate load tests are used, k{ may be found by one of the two ways,
1. A bearing pressure equal to not more than the ultimate pressure and the corresponding settlement is used for computing k1
2. Consider the bearing pressure corresponding to a settlement of 1.3 mm for computing kr
Estimation of k1Values
Plate load tests are both costly and time consuming. Generally a designer requires only the values
of the bending moments and shear forces within the foundation. With even a relatively large error in
the estimation of kr moments and shear forces can be calculated with little error (Terzaghi, 1955);
an error of 100 per cent in the estimation of ks may change the structural behavior of the foundation
by up to 15 per cent only.
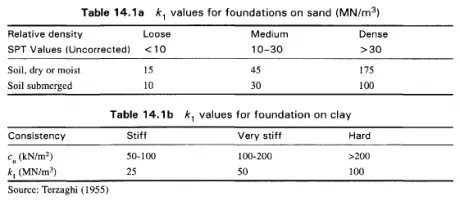
In the absence of plate load tests, estimated values of k1 and hence ks are used. The values suggested by Terzaghi for k1 (converted into S.I. units) are given in Table 14.1.