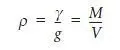Example 15.4
Assume that a compaction mold having a volume of 1/30 ft3 was filled with moist soil. The total weight
of the soil in the mold was found to be 4.10 lb. The soil was oven dried and its weight after drying was
3.53 lb. The specific gravity of solids was known to be 2.70. Water content, void ratio, porosity, degree
of saturation, total unit weight, and dry unit weight must be determined. A phase diagram is shown in
Fig. 15.5, with the known quantities in bold. The weight and volume of water are calculated as
Ww = W Ws = 4.10 3.53 = 0.57 lb
Vw Ww gw = § = 0.57 § 62.4 = 0.00913 ft3
The volume of solids is
If the same soil now becomes saturated by the addition of water at constant total volume, the saturated water content and saturated unit weight can be calculated as follows. The new volume of water is the entire void volume, 0.01238 ft3. Multiplying this value by 62.4 lb/ft3, the new weight of water is 0.77 lb. The water content at saturation is then

Note that the dry unit weight does not change if water is added without changing total volume.

Example 15.5 (SI units)
A soil sample has a volume of 2.5 liters (2.5 x 10^(3) m3) and a total mass of 4.85 kg. A water content test
indicates the water content is 28%. Assuming that the specific gravity of solids is 2.72, it is desired to
determine the total density, total unit weight, dry density, dry unit weight, void ratio, porosity, and degree
of saturation.
A phase diagram is shown in Fig. 15.6, with known values shown in bold.
Then
Va = V Vs Vw = 0.00250 0.00319 0.00106 = 0.00005 m3
The total density is
r = M / V = 4.850 kg / 0.00250 m3 = 1940 kg § m3
The total unit weight is