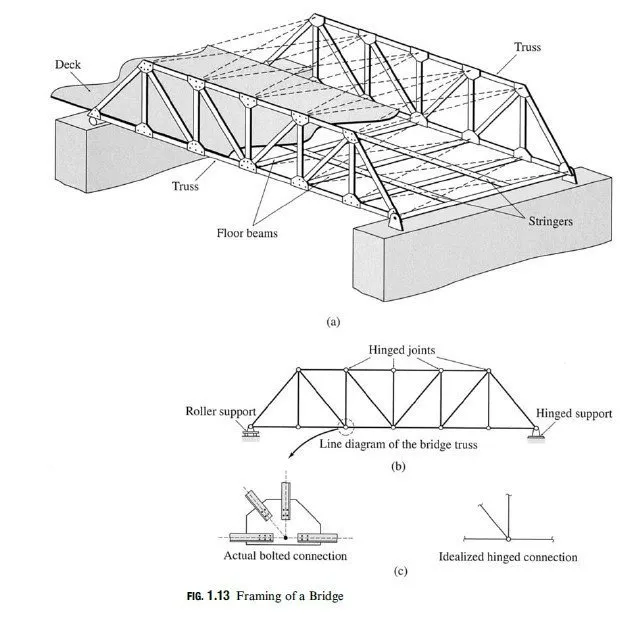
The method of joints, presented in the preceding section, proves to be very efficient when forces in all the members of a truss are to be determined. However, if the forces in only certain members of a truss are desired, the method of joints may not prove to be ancient, because it may involve calculation of forces in several other members of the truss before a joint is reached that can be analyzed for a desired member force. The method of sections enables us to determine forces in the specific members of trusses directly, without first calculating many unnecessary member forces, as may be required by the method of joints. The method of sections involves cutting the truss into two portions by passing an imaginary section through the members whose forces are desired. The desired member forces are then determined by considering the equilibrium of one of the two portions of the truss. Each portion of the truss is treated as a rigid body in equilibrium, under the action of any applied loads and reactions and the forces in the members that have been cut by the section. The unknown member forces are determined by applying the three equations of equilibrium to one of the two portions of the truss. There are only three equilibrium equations available, so they cannot be used to determine more than three unknown forces. Thus, in general, sections should be chosen that do not pass through more than three members with unknown forces. In some trusses, the arrangement of members may be such that by using sections that pass through more than three members with unknown forces, we can determine one or, at most, two unknown forces. Such sections are, however, employed in the analysis of only certain types of trusses (see Example 4.9).
Procedure for Analysis
The following step-by-step procedure can be used for determining the member forces of statically determinate plane trusses by the method of sections.
1. Select a section that passes through as many members as possible whose forces are desired, but not more than three members with unknown forces. The section should cut the truss into two parts.
2. Although either of the two portions of the truss can be used for computing the member forces, we should select the portion that will require the least amount of computational efort in determining the unknown forces. To avoid the necessity for the calculation of reactions, if one of the two portions of the truss does not have any reactions acting on it, then select this portion for the analysis of member forces and go to the next step. If both portions of the truss are attached to external supports, then calculate reactions by applying the equations of equilibrium and condition (if any) to the free body of the entire truss. Next, select the portion of the truss for analysis of member forces that has the least number of external loads and reactions applied to it.
3. Draw the free-body diagram of the portion of the truss selected, showing all external loads and reactions applied to it and the forces in the members that have been cut by the section. The unknown member forces are usually assumed to be tensile and are, therefore, shown on the free-body diagram by arrows pulling away from the joints.
4. Determine the unknown forces by applying the three equations of equilibrium. To avoid solving simultaneous equations, try to apply the equilibrium equations in such a manner that each equation involves only one unknown. This can sometimes be achieved by using the alternative systems of equilibrium equations (∑Fq = 0, ∑MA = 0, ∑MB = 0 or ∑MA = 0, ∑MB ¼ 0, ∑MC= 0) described in Section 3.1 instead of the usual two-force summations and a moment summation (∑Fx = 0, ∑Fy =0, PM = 0) system of equations.
5. Apply an alternative equilibrium equation, which was not used to compute member forces, to check the calculations. This alternative equation should preferably involve all three member forces determined by the analysis. If the analysis has been performed correctly, then this alternative equilibrium equation must be satisfied.