An analytical model is a simplified representation, or an ideal, of a real structure for the purpose of analysis. The objective of the model is to simplify the analysis of a complicated structure. The analytical model represents, as accurately as practically possible, the behavioral characteristics of the structure of interest to the analyst, while discarding much of the detail about the members, connections, and so on, that is expected to have little e¤ect on the desired characteristics. Establishment of the analytical model is one of the most important steps of the analysis process; it requires experience and knowledge of design practices in addition to a thorough understanding of the behavior of structures. Remember that the structural response predicted from the analysis of the model is valid only to the extent that the model represents the actual structure.
Development of the analytical model generally involves consideration of the following factors.

Plane Versus Space Structure

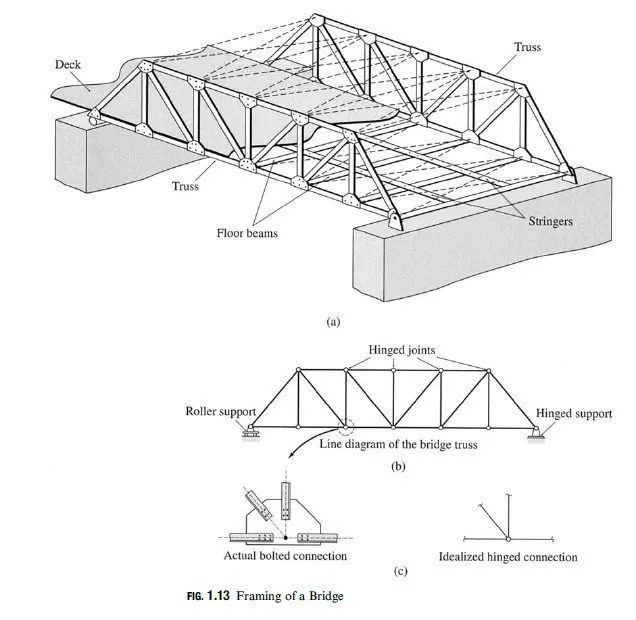
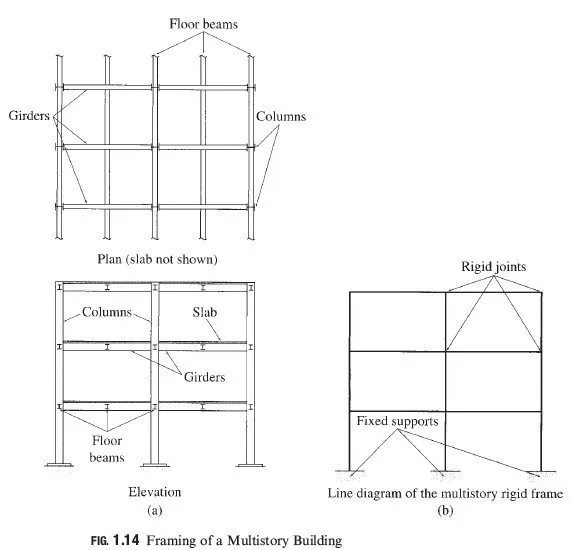
If all the members of a structure as well as the applied loads lie in a single plane, the structure is called a plane structure. The analysis of plane, or two-dimensional, structures is considerably simpler than the analysis of space, or three-dimensional, structures. Fortunately, many actual three-dimensional structures can be subdivided into plane structures for analysis. As an example, consider the framing system of a bridge shown in Fig. 1.13(a). The main members of the system, designed to support vertical loads, are shown by solid lines, whereas the secondary bracing members, necessary to resist lateral wind loads and to provide stability, are represented by dashed lines. The deck of the bridge rests on beams called stringers; these beams are supported by floor beams, which, in turn, are connected at their ends to the joints on the bottom panels of the two longitudinal trusses. Thus, the weight of the tra°c, deck, stringers, and floor beams is transmitted by the floor beams to the supporting trusses at their joints; the trusses, in turn, transmit the load to the foundation. Because this applied loading acts on each truss in its own plane, the trusses can be treated as plane structures. As another example, the framing system of a multistory building is shown in Fig. 1.14(a). At each story, the floor slab rests on floor beams, which transfer any load applied to the floor, the weight of the slab, and their own weight to the girders of the supporting rigid frames. This applied loading acts on each frame in its own plane, so each frame can, therefore, be analyzed as a plane structure. The loads thus transferred to each frame are further transmitted from the girders to the columns and then finally to the foundation. Although a great majority of actual three-dimensional structural systems can be subdivided into plane structures for the purpose of analysis, some structures, such as latticed domes, aerospace structures, and transmission towers, cannot, due to their shape, arrangement of members, or applied loading, be subdivided into planar components. Such structures, called space structures, are analyzed as three-dimensional bodies subjected to three-dimensional force systems.

Line Diagram

The analytical model of the two- or three-dimensional body selected for analysis is represented by a line diagram. On this diagram, each member of the structure is represented by a line coinciding with its centroidal axis. The dimensions of the members and the size of the connections are not shown on the diagram. The line diagrams of the bridge truss of Fig. 1.13(a), and the rigid frame of Fig. 1.14(a) are shown in Figs. 1.13(b) and 1.14(b), respectively. Note that two lines ( * * ) are sometimes used in this text to represent members on the line diagrams. This is done, when necessary, for clarity of presentation; in such cases, the distance between the lines does not represent the member depth.

Connection

Two types of connections are commonly used to join members of structures: (1) rigid connections and (2) flexible, or hinged, connections. (A third type of connection, termed a semirigid connection, although recognized by structural steel design codes, is not commonly used in practice and, therefore, is not considered in this text.)

A rigid connection or joint prevents relative translations and rotations of the member ends connected to it; that is, all member ends connected to a rigid joint have the same translation and rotation. In other words, the original angles between the members intersecting at a rigid joint are maintained after the structure has deformed under the action of loads. Such joints are, therefore, capable of transmitting forces as well as moments between the connected members. Rigid joints are usually represented by points at the intersections of members on the line diagram of the structure, as shown in Fig. 1.14(b). A hinged connection or joint prevents only relative translations of member ends connected to it; that is, all member ends connected to a hinged joint have the same translation but may have di¤erent rotations. Such joints are thus capable of transmitting forces but not moments between the connected members. Hinged joints are usually depicted by small circles at the intersections of members on the line diagram of the structure, as shown in Fig. 1.13(b).

The perfectly rigid connections and the perfectly flexible frictionless hinges used in the analysis are merely idealizations of the actual connections, which are seldom perfectly rigid or perfectly flexible (see Fig. 1.13(c)). However, actual bolted or welded connections are purposely designed to behave like the idealized cases. For example, the connections of trusses are designed with the centroidal axes of the members concurrent at a point, as shown in Fig. 1.13(c), to avoid eccentricities that may cause bending of members. For such cases, the analysis based on the idealized connections and supports (described in the following paragraph) generally yields satisfactory results.

Supports

Supports for plane structures are commonly idealized as either fixed supports, which do not allow any movement; hinged supports, which can prevent translation but permit rotation; or roller, or link, supports, which can prevent translation in only one direction. A more detailed description of the characteristics of these supports is presented in Chapter 3. The symbols commonly used to represent roller and hinged supports on line diagrams are shown in Fig. 1.13(b), and the symbol for fixed supports is depicted in Fig. 1.14(b).