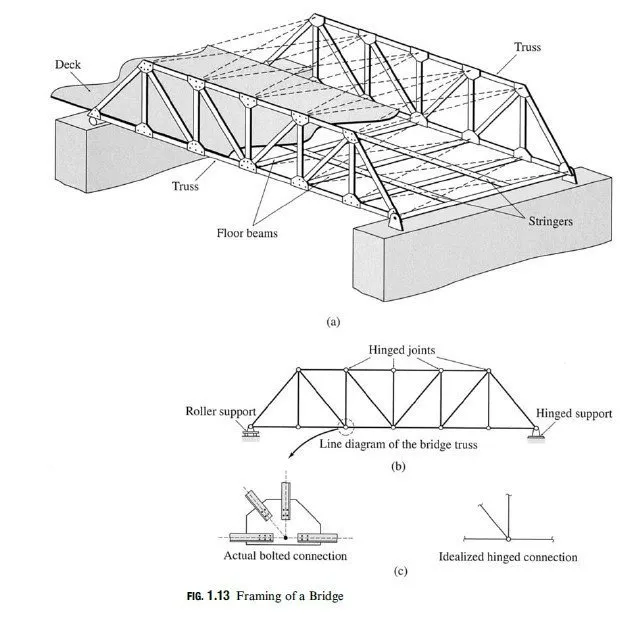
The principle of superposition simply states that on a linear elastic structure, the combined efect of several loads acting simultaneously is equal to the algebraic sum of the e¤ects of each load acting individually. For example, this principle implies, for the beam of Example 2, that the total reactions due to the two loads acting simultaneously could have been obtained by algebraically summing, or superimposing, the reactions due to each of the two loads acting individually.
The principle of superposition considerably simplifies the analysis of structures subjected to di¤erent types of loads acting simultaneously and is used extensively in structural analysis. The principle is valid for structures that satisfy the following two conditions: (1) the deformations of the structure must be so small that the equations of equilibrium can be based on the undeformed geometry of the structure; and (2) the structure must be composed of linearly elastic material; that is, the stressstrain relationship for the structural material must follow Hookes law. The structures that satisfy these two conditions respond linearly to applied loads and are referred to as linear elastic structures. Engineering structures are generally designed so that under service loads they undergo small deformations with stresses within the initial linear portions of the stress-strain curves of their materials. Thus, most common types of structures under service loads can be classified as linear elastic; therefore, the principle of superposition can be used in their analysis. The principle of superposition is considered valid throughout this text.