We consider a truss to be statically determinate if the forces in all its members, as well as all the external reactions, can be determined by using the equations of equilibrium.
Since the two methods of analysis presented in the following sections can be used to analyze only statically determinate trusses, it is important for the student to be able to recognize statically determinate trusses before proceeding with the analysis.

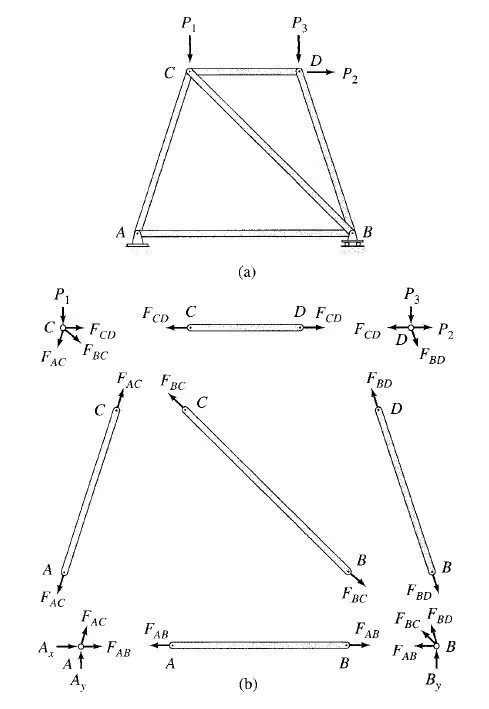
Consider a plane truss subjected to external loads P1; P2, and P3, as shown in Fig. 4.14(a). The free-body diagrams of the five members and the four joints are shown in Fig. 4.14(b). Each member is subjected to two axial forces at its ends, which are collinear (with the member centroidal axis) and equal in magnitude but opposite in sense. Note that in Fig. 4.14(b), all members are assumed to be in tension; that is, the forces are pulling on the members. The free-body diagrams of the joints show the same member forces but in opposite directions, in accordance with Newtons third law. The analysis of the truss involves the calculation of the magnitudes of the five member forces, FAB; FAC; FBC; FBD, and FCD (the lines of action of these forces are known), and the three reactions, Ax;Ay, and By. Therefore, the total number of unknown quantities to be determined is eight.

Because the entire truss is in equilibrium, each of its joints must also be in equilibrium. As shown in Fig. 4.14(b), at each joint the internal and external forces form a coplanar and concurrent force system, which must satisfy the two equations of equilibrium, ∑Fx =0 and ∑Fy =0. Since the truss contains four joints, the total number of equations available is 2(4)=8. These eight joint equilibrium equations can be solved to calculate the eight unknowns. The plane truss of Fig. 4.14(a) is, therefore, statically determinate.

Three equations of equilibrium of the entire truss as a rigid body could be written and solved for the three unknown reactions (Ax;Ay, and By). However, these equilibrium equations (as well as the equations of condition in the case of internally unstable trusses) are not independent from the joint equilibrium equations and do not contain any additional information.

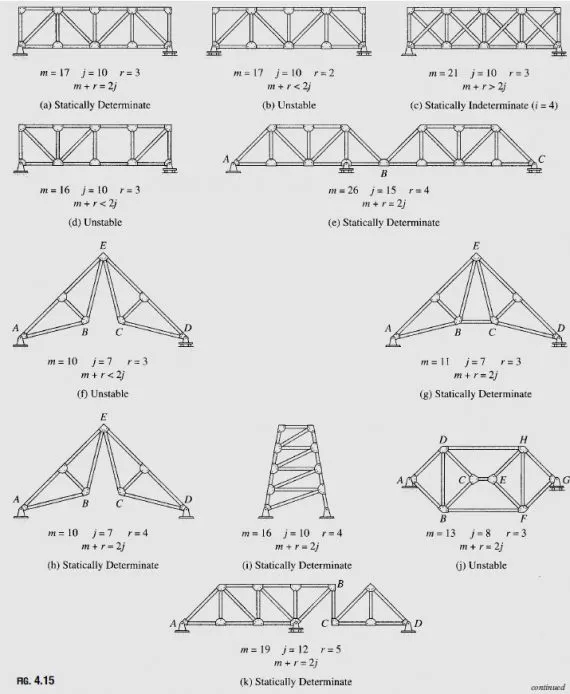
Based on the preceding discussion, we can develop the criteria for the static determinacy, indeterminacy, and instability of general plane trusses containing m members and j joints and supported by r (number of ) external reactions. For the analysis, we need to determine m member forces and r external reactions; that is, we need to calculate a total of m þ r unknown quantities. Since there are j joints and we can write two equations of equilibrium (∑Fx =0 and ∑Fy =0) for each joint, the total number of equilibrium equations available is 2j. If the number of unknowns (m+r) for a truss is equal to the number of equilibrium equations (2j)-that is, m+r>2j- all the unknowns can be determined by solving the equations of equilibrium, and the truss is statically determinate. If a truss has more unknowns ðm þ rÞ than the available equilibrium equations ð2jÞ that is, m + r > 2j all the unknowns cannot be determined by solving the available equations of equilibrium. Such a truss is called statically indeterminate. Statically indeterminate trusses have more members and/or external reactions than the minimum required for stability. The excess members and reactions are called redundants, and the number of excess members and reactions is referred to as the degree of static indeterminacy, i, which can be expressed as

i = (m+r)-2j [eq 4.3]

If the number of unknowns (m+r) for a truss is less than the number of equations of joint equilibrium (2j)-that is, m + r < 2j the truss is called statically unstable. The static instability may be due to the truss having fewer members than the minimum required for internal stability or due to an insufficient number of external reactions or both. The conditions of static instability, determinacy, and indeterminacy of plane trusses can be summarized as follows:

The first condition, for the static instability of trusses, is both necessary and sufficient in the sense that if m < 2j – r, the truss is definitely statically unstable. However, the remaining two conditions, for static determinacy (m=2j-r) and in determinacy (m>2j-r) are necessary but not sufficient conditions. In other words, these two equations simply tell us that the number of members and reactions is sufficient for stability. They do not provide any information regarding their arrangement. A truss may have sufficient number of members and external reactions but may still be unstable due to improper arrangement of members and/ or external supports.

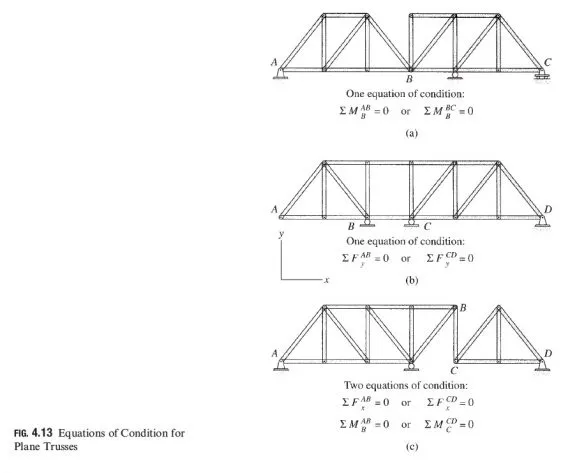
We emphasize that in order for the criteria for static determinacy and indeterminacy, as given by Eqs. (4.3) and (4.4), to be valid, the truss must be stable and act as a single rigid body under a general system of coplanar loads when attached to the supports. Internally stable trusses must be supported by at least three reactions, all of which must be neither parallel nor concurrent. If a truss is internally unstable, then it must be supported by reactions equal in number to at least three plus the number of equations of condition ð3 þ ecÞ, and all the reactions must be neither parallel nor concurrent. In addition, each joint, member, and portion of the truss must be constrained against all possible rigid body movements in the plane of the truss, either by the rest of the truss or by external supports. If a truss contains a sufficient number of members, but they are not properly arranged, the truss is said to have critical form. For some trusses, it may not be obvious from the drawings whether or not their members are arranged properly. However, if the member arrangement is improper, it will become evident during the analysis of the truss. The analysis of such unstable trusses will always lead to inconsistent, indeterminate, or infinite results.

Example 4.2

Classify each of the plane trusses shown in Fig. 4.15 as unstable, statically determinate, or statically indeterminate. If the truss is statically indeterminate, then determine the degree of static indeterminacy.

Solution