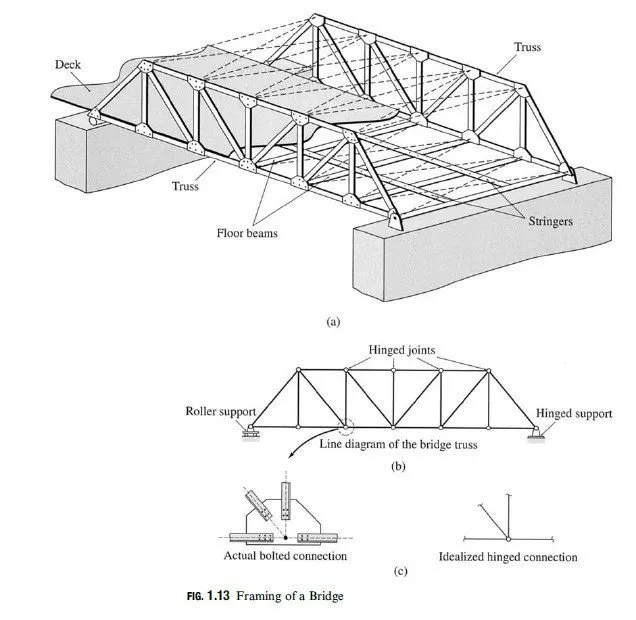
referred to as geometrically unstable externally. The two types of reaction arrangements that cause geometric instability in plane structures are shown in Fig. 3.12. The truss in Fig. 3.12(a) is supported by three parallel reactions. It can be seen from this figure that although there is a succient number of reactions r = 3 all of them are in the vertical direction, so they cannot prevent translation of the structure in the horizontal direction. The truss is, therefore, geometrically unstable. The other type of reaction arrangement that causes geometric instability is shown in Fig. 3.12(b). In this case, the beam is supported by three nonparallel reactions. However, since the lines of action of all three reaction forces are concurrent at the same point, A, they cannot prevent rotation of the beam about point A. In other words, the moment equilibrium equation ∑MA = 0 cannot be satisfied for a general system of coplanar loads applied to the beam. The beam is, therefore, geometrically unstable. Based on the preceding discussion, we can conclude that in order for a plane internally stable structure to be geometrically stable externally so that it can remain in equilibrium under the action of any arbitrary coplanar loads, it must be supported by at least three reactions, all of which must be neither parallel nor concurrent.

Static Determinacy of Internally Unstable Structures Equations of Condition

Consider an internally unstable structure composed of two rigid members AB and BC connected by an internal hinge at B, as shown in Fig. 3.13(a). The structure is supported by a roller support at A and a hinged support at C, which provide three nonparallel nonconcurrent external reactions. As this figure indicates, these reactions, which would have been su°cient to fully constrain an internally stable or rigid structure, are not su°cient for this structure. The structure can, however, be made externally stable by replacing the roller support at A by a hinged support to prevent the horizontal movement of end A of the structure. Thus, as shown in Fig. 3.13(b), the minimum number of external reactions required to fully constrain this structure is four. Obviously, the three equilibrium equations are not su°cient to determine the four unknown reactions at the supports for this structure. However, the presence of the internal hinge at B yields an additional equation that can be used with the three equilibrium equations to

determine the four unknowns. The additional equation is based on the condition that an internal hinge cannot transmit moment; that is, the moments at the ends of the parts of the structure connected to a hinged joint are zero. Therefore, when an internal hinge is used to connect two portions of a structure, the algebraic sum of the moments about the hinge of the loads and reactions acting on each portion of the structure on either side of the hinge must be zero. Thus, for the structure of Fig. 3.13(b), the presence of the internal hinge at B requires that the algebraic sum of moments about B of the loads and reactions acting on the individual members AB and BC must be zero; that is,

These two equations of condition can be used in conjunction with the three equilibrium equations to determine the five unknown external reactions. Thus, the structure of Fig. 3.13(c) is statically determinate externally. From the foregoing discussion, we can conclude that if there are ec equations of condition (one equation for each internal hinge and two equations for each internal roller) for an internally unstable structure, which is supported by r external reactions, then if