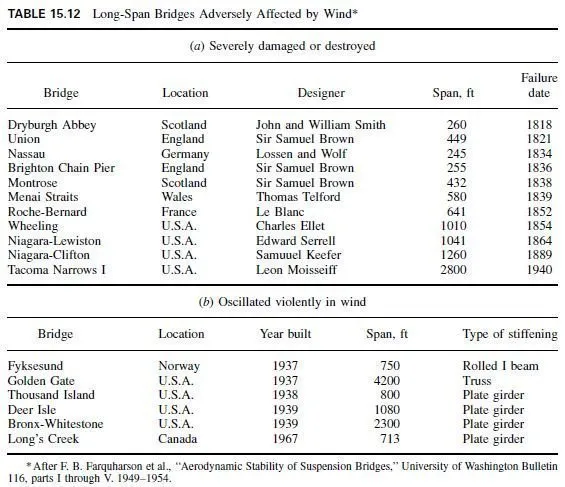
A force acting on a body may have a tendency to rotate it. The measure of this tendency is
the moment of the force about the axis of rotation. The moment of a force about a specific point equals the product of the magnitude of the force and the normal distance between the point and the line of action of the force.
Moment is a vector.
Suppose a force F acts at a point A on a rigid body (Fig. 3.5). For an axis through an arbitrary point O and parallel to the z axis, the magnitude of the moment M of F about this axis is the product of the magnitude F and the normal distance, or moment arm, d.

The distance d between point O and the line of action of F can often be difficult to calculate.
Computations may be simplified, however, with the use of Varignons theorem, which states that the moment of the resultant of any force system about any axis equals the algebraic sum of the moments of the components of the force system about the same axis. For the case shown the magnitude of the moment M may then be calculated as
Because the component Fz is parallel to the axis through O, it has no tendency to rotate the body about this axis and hence does not produce any additional moment.
In general, any force system can be replaced by a single force and a moment. In some
cases, the resultant may only be a moment, while for the special case of all forces being concurrent, the resultant will only be a force.
For example, the force system shown in Figure 3.6a can be resolved into the equivalent
force and moment system shown in Fig. 3.6b. The force F would have components Fx and
Fy as follows:
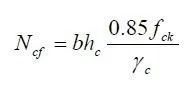
The magnitude of the resultant force F can then be determined from
![]()
With Varignons theorem, the magnitude of moment M may then be calculated from
![]()
with d1 and d2 defined as the moment arms in Fig. 3.6c. Note that the direction of the
moment would be determined by the sign of Eq. (3.9); with a right-hand convention, positive
would be a counterclockwise and negative a clockwise rotation. This force and moment could further be used to compute the line of action of the resultant of the forces F1 and F2 (Fig. 3.6d). The moment arm d could be calculated as
d= M/F
It should be noted that the four force systems shown in Fig. 3.6 are equivalent.