In buildings, splices of members subjected principally to shear should develop the strength required by the stresses at point of splice. For groove welds, however, the full strength of the smaller spliced member should be developed.
In highway bridges, shear splices should be designed for the larger of the following: 75% of the strength of the member or the average of the calculated stress at point of splice and the strength of the member there. Splices of rolled flexural members, however, may be designed for the calculated maximum shear multiplied by the ratio of splice design moment to actual moment at the splice.
In railroad bridges, shear splices in main members should have the same strength as the
members. Splices in secondary members should develop the average of the strength of the
members and the calculated stresses at the splices.
When fillers are used, the requirements discussed in Art. 5.13 should be satisfied.
Shear splices may be made with complete-penetration groove welds, preferably without splice plates. Design rules for groove welds are practically the same as for compression
splices (Art. 5.27), though values of allowable stresses are different.
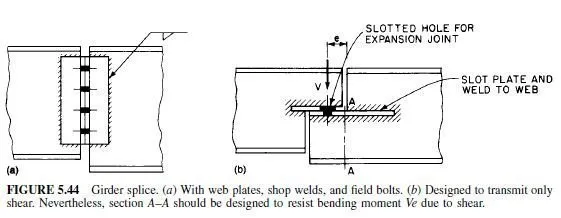
Shear splices are most often used for splicing girder webs. In such applications, splice plates should be symmetrically arranged on opposite sides of the web. For bridges, they should extend the full depth of the girder between flanges. Bolted splices should have at least two rows of fasteners on each side of the joint.
Generally, it is desirable to locate flange and web splices at different sections of a girder.
But this is not always practical. Long continuous girders, for example, often require a field splice, which preferably is placed at a section with low bending stresses, such as the deadload inflection points. In such cases it could be troublesome and costly to separate flange and web splices.
Sometimes, a web splice can be placed where it is required to transmit only shear. Usually, however, a web splice must be designed for both shear and moment. Even in a web splice subjected to pure shear, moment is present if splice plates are used, because of the eccentricity of the shear. For example, as indicated in Fig. 5.42, a group of fasteners on one side of the joint transmits the shear V (kips) from the web to the splice plates. This shear acts through the center of gravity O of the fastener group. On the other side of the joint, a similar group of fasteners transmits the shear from the splice plates to the web on that side. This shear acts through the center of gravity of that fastener group. The two transmitted shears, then, form a couple 2Ve, where e is half the distance between the shears. This moment must be taken by the fasteners in both groups. In the design of a splice, however, it generally is simpler to work with only one side of the joint. Hence, when the forces on one fastener group are computed, the fasteners should be required to carry the shear V plus a moment Ve. (In a symmetrical splice, e is the distance from O to the splice.)
The classical elastic method assumes that in resisting the moment, each fastener in the
group tends to rotate about O. As a consequence:
The reaction Pb of each fastener acts normal to the radius vector from O to the fastener
(Fig. 5.42).
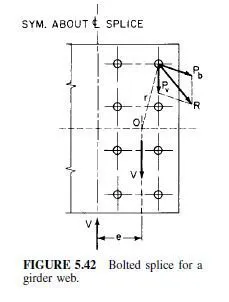
The magnitude of Pb is proportional to the distance r from O.
The resisting moment provided by each fastener is proportional to its distance from O.
The applied moment equals the total resisting moment, the sum of the resisting moments
of the fasteners in the group,
These consequences result in the relationship

Hence, when the moment applied to a fastener group is known, the maximum stress in the
fasteners can be computed from Eq. (5.13).
This stress has to be added vectorially to the shear on the fastener (Fig. 5.42). The shear (kips) is given by

where n is the number of fasteners in group. The resultant stress must be less than the allowable capacity of the fastener.
Depending on the fastener pattern, the largest resultant stress does not necessarily occur in the outermost fastener. Vectorial addition of shear and bending stresses may have to be performed for the most critical fasteners in a group to determine the maximum.
In computing the fastener stresses, designers generally find that the computations are simpler if the forces and distances are resolved into their horizontal and vertical components.
Advantage can be taken of the fact that

Alternative Splices. Bolted splices may be made in several different ways when moment is not to be transmitted across the joint. Figure 5.44 shows two examples.
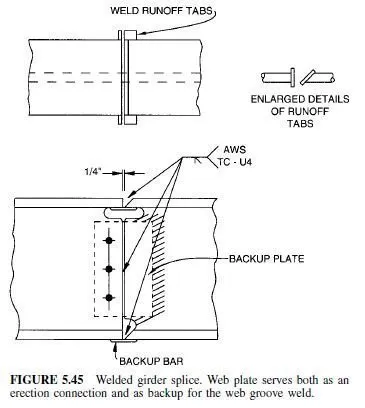
Field-bolted splices generally are more economical than field-welded splices. Groove welds may be more economical, however, if they are made in the shop. Field welding is complicated by the need to control the welding sequence to minimize residual stresses. This often requires that flange-to-web welds on each side of the joint be omitted during fabrication and made after the splice welds. Also, the web interferes with the groove welding of the flange. To avoid the risk of a poor weld, the web must be coped (Fig. 5.45). This provides space for welding, backup bars, cleaning, and other necessary operations.