9.1 Categories and properties of projections Chapter 8 has shown that it is useful to express the 3D positions of points near the earths surface in terms of latitude, longitude and height above an ellipsoid of defined shape. This system gives a precise and straightforward definition of any points location, in terms of parameters (east, north and up1) which are convenient to use everywhere around the world. It is often necessary to record the positions of points, boundaries and natural features such as coastlines, on a map and this too is usually done by showing the (east, north) positions directly on a flat 2D projection, and (where necessary) the heights by means of contour lines, etc. The complication which arises is that the surface of any ellipsoid, including a sphere, is doubly curved, and therefore cannot be developed (i.e. unwrapped) to form a planar projection. One solution is to project the surface features of the ellipsoid directly onto a plane; alternatively, they can be projected onto a developable surface such as a cylinder or cone, which is then developed to give a planar projection. In each case, the resulting projection can subsequently be scaled down to give a map of a useful size. It is not possible to project a doubly curved surface onto a planar or developable surface in such a way that the scale of the projection is unity (or any other constant value) at all places. Thus, all such projections involve some degree of distortion on the resulting map, except at certain points or along particular lines. By varying the exact method of projection, it is possible to manipulate the changes in scale so as to avoid some aspects of distortion on a map, but usually at the expense of increased distortion in other respects. In particular, there are three important properties which maps may have; they are as follows: 1 A conformal projection manages the scaling effects such that, at any point on the projection, the scale in all directions is the same.2 Such maps are also orthomorphic, which means that small shapes on the ground (buildings, etc.) are shown as the same shape on the map. The result of this is that the angles at which two lines cross on the earths surface are preserved exactly on the map. However, the shortest distance over the ellipsoid between two distant points (a geodesic) does not in general plot as a straight line on the map. 2 An equal area projection manages scaling such that if the scale at a point is increased in one direction, then it is reduced in another. Thus, the area of any feature on an equal area map (e.g. a state) is preserved exactly, subject to the quoted scale of the map. 1 Not exactly up as defined by a plumb bob, as the ellipsoid is not necessarily exactly parallel to the geoid. 2 This scale is called the scale factor and is greater than 1 if the size on the projection is greater than the size on the ellipsoid.
However, the shape of the area will not be preserved exactly; and at any point on the map, the scale in one direction (e.g. north-south) will generally differ from the scale in any other direction (e.g. east-west). Small circles drawn on the surface of the earth would plot as ellipses of the same area on the projection, but with greater eccentricity in places where the distortion of the projection is higher. 3 In an equidistant projection, the scale of the projection is maintained at unity along a particular set of geodesics. Equidistant projections are normally azimuthal projections (see below) then, the scale is preserved along all geodesics radiating out from the central point of the projection. These geodesics also plot as straight lines, so that distances from the central point to any other point on the map can be measured directly. However, all other geodesics will plot as curved lines on the map. No projection can have more than one of these properties over an extended area, and some have none of them, preferring instead to strike a compromise between them. Conformal projections are generally preferred for surveying purposes, because angles measured in the field (with total stations, etc.) can be plotted directly onto the map. Apart from these properties, there are three important classes of projection, depending on the surface onto which the initial projection is made. These are described below.
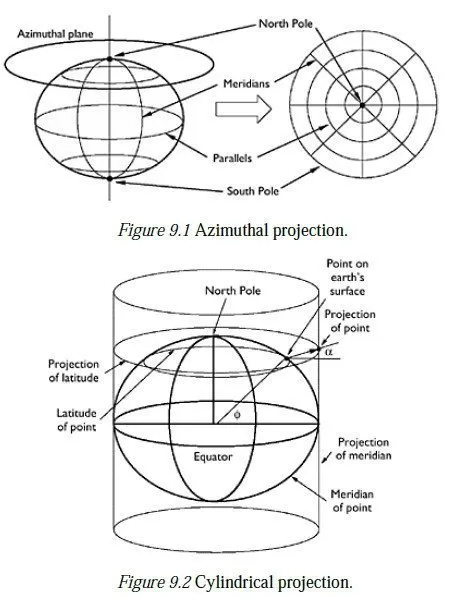
Azimuthal projections
At any point on the earths surface, the azimuthal plane is defined as the plane passing through the point and lying normal to the vertical at that point. An azimuthal projection involves projecting the surrounding region onto that plane; this can be done so as to give a conformal, equal area or equidistant projection. An azimuthal projection at the North Pole (Figure 9.1) would show the North Pole as a central point, with lines of constant latitude (known as parallels) appearing as concentric circles around it. If the whole world was projected, the South Pole would appear as the outermost circle.3 Meridians would appear as radial lines, crossing the parallels at 90°. Azimuthal projections can be made at any point on the earths surface and have the advantage of having distortion which is zero at the central point and increases as a function of distance from that point. They are thus suitable for mapping countries or regions which are approximately circular in shape. However, Azimuthal projections at points other than the Poles would normally treat the earth as a sphere rather than an ellipsoid, to simplify the projection algebra. This makes them unsuitable for highprecision surveying work on a large scale (over 100 km, say), because it is inappropriate to model the geoid as a spherical surface over large areas.
Cylindrical projections
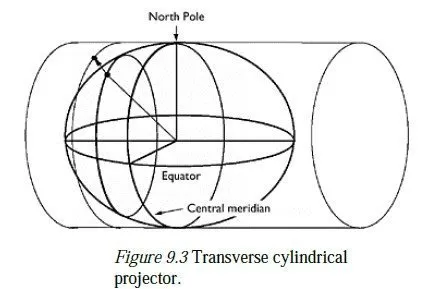
The classical cylindrical projection can be visualised as wrapping a sheet of paper round the earths equator to form a cylinder and projecting points on the earths surface out onto it, as shown in Figure 9.2. The projection angle, α, is a function of the latitude,Φ , of a given point; the function can be defined so as to give an equal area projection or a conformal projection.
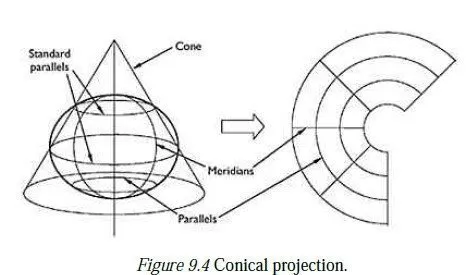
When the paper is unwrapped, the resulting projection shows parallels as straight horizontal lines and meridians as straight, equally spaced vertical lines. This type of projection has no distortion on the equator and low distortion nearby, and so is particularly suitable for mapping tropical countries. The transverse form of a cylindrical projection involves wrapping the sheet of paper round a meridian (called the central meridian) rather than the equator, as shown in Figure 9.3. (Actually, this is not strictly a cylindrical projection, since meridians on an ellipsoid are not exactly circular.) Transverse cylindrical projections give maps which have no distortion on the central meridian and low distortion nearby, and so are suitable for countries at any latitude which lie in a predominantly north-south direction (e.g. the British Isles). Oblique cylindrical projections also exist, in which the earth is treated as a sphere rather than an ellipsoid, and the cylinder touches its surface round a great circle other than a meridian or the equator. Such projections are useful for mapping countries which lie along such a line.
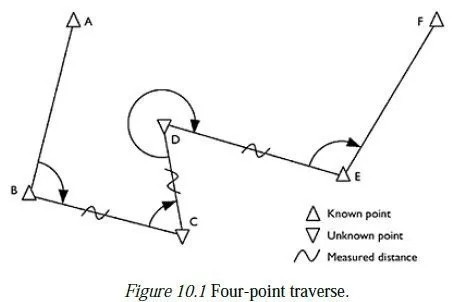
Conical projections
Conical projections are generally made onto a cone whose axis passes through the North and South Poles, and whose surface passes through the surface of the earth along two parallels, known as the standard parallels. Points on the earths surface are projected onto the cone which is then developed to give a map of the shape shown in Figure 9.4. As in an azimuthal projection, the lines of constant latitude are concentric circular arcs, and the meridians are straight radial lines at right angles to the arcs. The spacing of the parallels can be arranged to give a projection which is conformal, equal area or equidistant (with the central pole as the reference point).
The resulting projection has no distortion of shape or scale on the standard parallels and low distortion near to them. A suitable choice of standard parallels can thus give a minimum-distortion projection of a country running in a predominantly east-west direction, such as the United States of America.
The angle between neighbouring meridians, and thus the shape of the developed map, depends on the shape of the initial cone (which in turn depends on which two parallels are chosen as the standard parallels). At one extreme, the cone becomes a flat circular disc and the result is an azimuthal projection, as described above. At the other extreme, the cone becomes a cylinder, either touching just at the equator or cutting parallels which are equally spaced north and south of it this, of course, is a cylindrical projection.